Учебное пособие: Системы линейных уравнений и неравенств

Основные вопросы лекции: основные понятия и определения теории систем уравнений; система n линейных уравнений с n неизвестными; метод обратной матрицы; метод Крамера; метод Гаусса; теорема Кронекера-Капелли; система n линейных уравнений с m неизвестными; однородные системы линейных уравнений; фундаментальная система решений; структура общего решения.

Система mлинейных уравнений с nпеременными имеет вид:

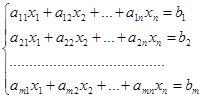
или

(1)

где a₁₁ , a₁₂ , … , a_mn — произвольные числа, называемые соответственно коэффициентами при переменных и b₁ ,b₂ , … , b_m - свободными членами уравнений.

Решением системы(1) называется такая совокупность nчисел х₁ , х₂ , ... , х_n , при подстановке которых каждое уравнение системы обращается в верное равенство.

Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.

Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Запишем систему (1) в матричной форме. Обозначим:

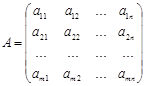; В=(b₁ , b₂ , … , b_n )^т ; Х=(x₁ , x₂ , … , x_n )^т

где А— матрица коэффициентов при переменных, или матрица системы, X — матрица-столбец переменных; В — матрица-столбец свободных членов.

На основании определения равенства матриц систему (1) можно записать в виде:

А*Х=B (2)

А матрица состоящая из А, В, Х матриц называется расширенной матрицей:

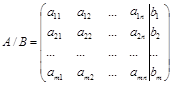- расширенная матрица.

Метод Гаусса — метод последовательного исключения переменных — заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

Рассмотрим решение системы (1) mлинейных уравнений с nпеременными в общем виде:

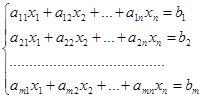(3)

Если m=n, то рассмотрим расширенную матрицу. Учитывая правую часть, приведем данную матрицу к треугольному виду:

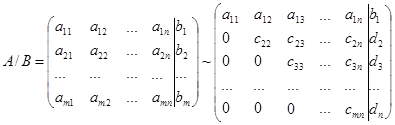
Ситема линейных уравнении соотвествующее данной матрице запишем в следуюшем виде

(4)

Если в данном уравнении c_nn ≠0, c_n-1n-1 ≠0, ... , c₃₃ ≠0, c₂₂ ≠0, a₁₁ ≠0 то, в первую очередь найдем

x_n , а затем постепенно поднимаясь находим остольные решения - x_n-1 , … , x₃ , x₂ , x₁ .

Формула Крамера

Теорема Крамера. Пусть |A|— определитель матрицы системы А, а Δ_j — определитель матрицы, получаемой из матрицы А заменой j-го столбца столбцом свободных членов. Тогда, если Δ ≠0, то система имеет единственное решение, определяемое по формулам:

(5)

Формулы (5) получили название формул Крамера.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--