Учебное пособие: Теория алгоритмов

Дуги, исходящие из операторных вершин, подсоединяются либо к первой вершине – распознавателю, либо к выходной вершине. В первом случае подстановка называется обычной, во втором – заключительной.

Кроме того, имеются входная и выходная вершины. Входная вершина связана дугой с первым распознавателем.

На вход графа подается некоторое входное слово p.

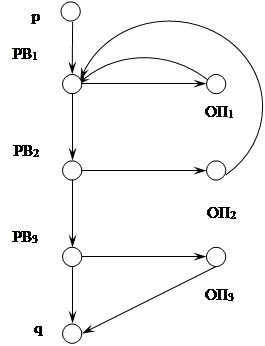
Пример. Граф для трех подстановок (к = 3) (рис.1) имеет три распознавателя (РВ1,РВ2,РВ3) и три операторные вершины (ОП1,ОП2,ОП3).

Если подстановки заданы как ba ® ab, bc ® ba, bb ® ac, а входное слово

р = bcbaab, то работа алгоритма будет иметь следующий вид.

Пpимеp. Задан алфавит А={+, 1} и система подстановок:

‘1+1’ ® ‘11’ , ‘1’®`1`.

Обычная Заключительная

подстановка подстановка

Пусть дано входное слово р = ’11+11+1’. Оно перерабатывается алгоритмом в строку:

‘11+11+1’ ® ‘1111+1’ ® ‘11111’ ® `11111` !

Алгоритм реализует сложение единиц.

Тезис Маркова

Для любого алгоритма в произвольном конечном алфавите А можно построить эквивалентный ему нормальный алгоритм.

Все известные до сих пор алгоритмы нормализуемы.

Машина Тьюринга

Одно из уточнений понятий алгоритма было дано Э. Постом и А. Тьюрингом независимо друг от друга в 1936-1937гг. Основная мысль их заключалась в том, что алгоритмические процессы – это процессы, которые может свершить подходящим образом устроенная ”машина”. Ими были описаны гипотетические (условные) устройства, которые получили название «Машина Поста» и «Машина Тьюринга»(МТ). Так как в них много общего, то рассмотрим только машину Тьюринга.

Машина Тьюринга состоит из следующих частей:

1. Информационной ленты, представляющей бесконечную память машины. Это бесконечная лента, разделенная на ячейки. В каждой ячейке можно поместить лишь один символ из возможного их множества S={S₁ ,S₂ ,….,S_m },которое составляет внешний алфавит МТ. В этом алфавите один из символов (пусть это будет S₁ ) соответствует пустому символу.

2. Считывающей головки – чувствительного специального элемента, способного обозревать содержимое ячеек. Лента может перемещаться вдоль головки так, что в каждый момент времени головка обозревает одну ячейку.

3. Управляющего устройства (УУ), которое в каждый момент времени находится в некотором состоянии. Число состояний конечно. Обозначим множество состояний как {q₁ ,q₂ ,…,q_n }. Среди состояний одно соответствует заключительному, при котором МТ останавливается. УУ связано со считывающей головкой.

Кроме того, УУ вырабатывает три команды на перемещение ленты: П, Л, Н, где

П – переместиться на соседнюю справа ячейку;

Л – переместиться соседнюю слева ячейку;

Н – продолжать обозревать ту же ячейку.

Совокупность символов {q₁ ,q₂ ,…,q_n } и {П,Л,Н} образуют внутренний алфавит МТ.

Работа машины происходит в дискретном времени. В начальный момент времени в ограниченный участок ленты записано слово в алфавите S, представляющее исходное условие задачи. В остальных ячейках предполагается записанным пустой символ. Управляющее устройство находится в начальном состоянии q₁ . На каждом шаге работы МТ обозревает на ленте символ S_k и в зависимости от него и от состояния q_i , переходит в состояние q_j , заменяет S_k на символ S_l и передвигает ленту (либо нет) на одну ячейку.

Каждая элементарная операция имеет вид