Учебное пособие: Теория алгоритмов

Множество элементарных операций упорядочено и образует абстрактную программу, которая представляет алгоритм.

Считывающая головка и управляющее устройство образуют логический блок, который представляет собой (2,3)-полюсник.

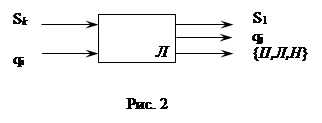
Структура МТ имеет следующий вид:

S1

S2

…

Sk

…

Sm

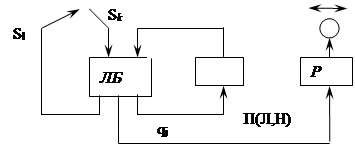
Q - ячейка хранит символ состояния, а Р - ячейка – символ сдвига. В них происходит задержка данных символов до начала следующего такта.

В качестве начальной информации на ленту можно записать любую конечную последовательность символов (входное слово) U внешнего алфавита. В начале работы алгоритма устройство управления находится в начальном состоянии, головка обозревает первый слева непустой символ входного слова U. Если после конечного числа тактов МТ останавливается, переходя в заключительное состояние, а на ленте оказывается информация B, то говорят, что машина применима к последовательности U и перерабатывает ее в последовательность B.

Если остановка и сигнал об остановке никогда не поступают, то говорят, что МТ не применима к последовательности U.

Рассмотрим функционирование МТ на примере сложения двух чисел, которые будем изображать в виде набора единиц.

Внешний алфавит будет состоять из символов: {1, +, Ù}, где Ù – пустой символ.

Внутренний алфавит будет состоять из четырех символов {q₁ , q₂ , q₃ , !}, где символ q₁ означает начальное состояние, а ! – заключительное состояние.

Пусть на ленте записана начальная информация:

1	2	3	4	5	6	7
1	1	+	1

МТ должна ее переработать в результирующую информацию:

1	2	3	4	5	6	7
1	1	1

Абстрактная программа, реализующий операцию сложения, будет иметь вид:

1q1 →Ùq3 П 1q3 →1q3 П +q3 →+q3 П

Ùq3 →1q2 H +q2 →+q2 Л 1q2 →1q2 Л Ùq2 →Ùq1 П +q1 →Ù!Н

Начальное состояние УУ=q1, состояние ленты имеет вид:

1	2	3	4	5	6	7
1	1	+	1

После первого шага состояние YY=q3, состояние ленты как на рис.

1	2	3	4	5	6	7
1	+	1

1	2	3	4	5	6	7
1	+	1	1

После пятого шага YY перейдёт в состояние q2. Состояние ленты показано на рис.

После десятого шага YY в состоянии q1 (рис. )

1	2	3	4	5	6	7
1	+	1	1

Последовательность команд, реализующих операцию сложения, удобно задать таблицей, которую называют функциональной схемой алгоритма.

q1	q2	q3
1	Ùq3 П	1q2 Л	1q3 П
Ù	Ùq1 П	Ùq1 П	1q2 H
+	Ù!Н	+q2 Л	+q3 П

Основная гипотеза теории алгоритмов (тезис Чёрча)

Всякий алгоритм может быть задан посредством тьюринговой функциональной схемы и реализован в соответствующей машине Тьюринга.

Обоснование гипотезы.

Речь не идет о доказательстве гипотезы, так как она содержит не формализованные математические понятия.