Учебное пособие: Виявлення грубих результатів вимірювань

При значеннях довірчої ймовірності та залежність коефіцієнта від числа складових m незначна, тому рекомендується брати середні значення коефіцієнта : . При залежність коефіцієнта від числа складових m та їх співвідношення істотні, тому при рекомендується брати значення , а при можна уточнювати значення за графіком (наводиться в окремих працях) або за допомогою табл. 2.3.

Таблиця 2.2

Довірча ймовірність, P	Значення коефіцієнта при числі складових m, що дорівнює:
	2	3	4	5	...	¥	Середнє
0,90	0,97	0,96	0,95	0,95	...	0,95	0,95
0,95	1,10	1,12	1,12	1,12	...	1,13	1,13
0,99	1,27	1,37	1,41	1,42	...	1,49	1,4

Таблиця 2.3

Число cкладових, m	Значення коефіцієнта kq при співвідношенні границь , що дорівнює:
	0	1/2	1	2	3	4	5	6	7
2	0,98	1,15	1,27	1,22	1,15	1,12	1,08	1,07	1,05
3	1,27	1,32	1,37	1,32	1,24	1,18	1,15	1,12	1,08
4	1,38	1,40	1,41	1,36	1,28	1,23	1,18	1,15	1,11

Параметр , який характеризує співвідношення складових невилученої систематичної похибки, дорівнює найменшому із співвідношень границь та , при цьому .

При малому числі складових () після знаходження статистичної границі q_д необхідно порівняти її з арифметичною границею q_а і прийняти як остаточну найменшу з двох границь. Слід зазначити, що для малого числа складових арифметичні границі q_а звичайно незначно перевищують статистичні q_д — не більше як на 30 %, що в багатьох випадках цілком припустимо.

Якщо невилучені систематичні складові похибки задані своїми довірчими границями , обчисленими за формулою (2.22), то довірчу границю сумарної систематичної похибки знаходять із виразу

,

де - довірчі границі j-ї невилученої систематичної складової похибки, що відповідають довірчій ймовірності ;

- квантильний коефіцієнт переходу, що відповідає довірчій імовірності .

2.9.3. Визначення сумарної випадкової похибки вимірювань

В основу підсумовування випадкових складових похибки вимірювань покладена властивість дисперсії для суми залежних випадкових величин, яка стосовно похибок записується так:

, (2.23)

де - дисперсія суми n випадкових похибок;

- дисперсія j-ї складової випадкової похибки, ;

- взаємна кореляційна функція, або взаємний кореляційний момент j‑ї та l -ї складових випадкової похибки, причому запис означає, що підсумовування розповсюджується на всі можливі попарні сполучення складових, для яких . Взаємна кореляційна функція визначається рівнянням

, (2.24)

де - відповідно СКВ (або їх оцінки ) j-ї та l -ї складових випадкової похибки:

;

- нормована взаємна кореляційна функція, або коефіцієнт кореляції:

.

Переходячи у формулі (2.23) до СКВ випадкових похибок з урахуванням (2.24), одержимо вираз для обчислення СКВ сумарної випадкової похибки за її складовими

. (2.25)

Звернемо увагу на те, що ця формула підсумовування випадкових похибок є універсальною, оскільки СКВ (і дисперсія) не залежить від закону розподілу похибок.

Відзначимо, що строго врахувати всі кореляційні зв’язки, а отже, і точно визначити коефіцієнт кореляції між похибками досить складно і не завжди можливо. Так, коефіцієнт кореляції між величинами визначається виразом

,

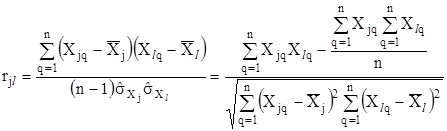де - результати q-го спостереження величин , відповідно, ;