Учебное пособие: Виявлення грубих результатів вимірювань

За степенем корельованості випадкові похибки слід розділити лише на два види: сильно корельовані і слабко корельовані. Умовною границею між сильною і слабкою кореляціями випадкових похибок вважають умову . Враховуючи це, до сильно корельованих належать похибки, для яких , і для них приймають . Прикладами сильно або жорстко корельованих похибок є похибки, викликані однаковою причиною (загальним джерелом живлення, майже однаковим впливом змінювання температури і т.п.), і в інших випадках, коли тісні кореляційні зв’язки між похибками явно проглядаються. До слабко корельованих належать похибки, для яких і для них приймають . Такі похибки звичайно викликаються різними причинами, причому такими, що не мають між собою явного зв’язку. Вони також називаються незалежними. Проміжні значення коефіцієнта кореляції, тобто крім або , при оцінюванні випадкової похибки, як правило, не використовуються.

У практиці вимірювань здебільшого мають справу з незалежними випадковими похибками, для яких і формула (2.25) набуває вигляду

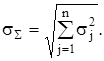(2.26)

Якщо СКВ похибки визначити у відносних одиницях, то

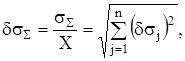(2.27)

де - відносне СКВ j-ї складової похибки.

Інколи для спрощення розрахунків переходять від підсумовування дисперсій (або СКВ) випадкових похибок до підсумовування максимальних (допустимих) значень абсолютних похибок . Тоді аналогічно формулам (2.22) і (2.26) маємо

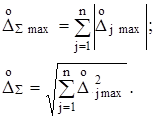(2.28)

Формула для СКЗ сумарної випадкової похибки дає завищену оцінку в порівнянні з (2.26), але ця оцінка більш вірогідна, ніж "оцінка зверху" .

Таким чином, арифметичне підсумовування використовується для грубої оцінки сумарної похибки, названої "оцінкою зверху" (або за максимумом), і при випадковому характері похибок. Воно зводиться до підсумовування максимальних значень окремих складових похибок. При такому підході передбачається, що всі складові випадкової похибки мають одночасно і максимальне значення, і однаковий знак. Очевидно, ймовірність такого збігу дуже мала, тому арифметичне підсумовування дає завищену оцінку сумарної випадкової похибки, і похибка цієї оцінки буде тим істотніша, чим більше число складових підсумовується. Тому арифметичне підсумовування випадкових похибок можливе при грубій оцінці сумарної похибки, коли вона містить 2-3 складових.

Переходячи в (2.28) до відносних похибок, маємо

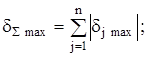
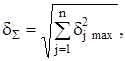
де

При умові формула (2.25) набуває вигляду

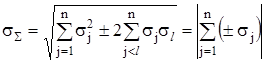, (2.29)

де знак "+" означає, що для складових з позитивною кореляцією () СКВ треба брати зі знаком "+", а для складових з негативною кореляцією брати зі знаком "-". Знак модуля належить до .

Зокрема, при підсумовуванні двох складових випадкової похибки, СКВ яких , з (2.29) маємо

,

тобто наявність жорсткої кореляції () між випадковими складовими похибки приводить до переходу від геометричного їх підсумовування до алгебраїчного.

Таким чином, при виборі того або іншого методу (правила) підсумовування складових похибки визначальною ознакою є не розділ їх на систематичні і випадкові, а ступінь (рівень) кореляційних зв’язків: сильний або слабкий.

Якщо для складових випадкової похибки задано границі довірчих інтервалів і довірчі ймовірності , то СКВ кожної із складових, згідно з виразом (2.9), знаходять за формулою

.

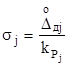Якщо всі складові випадкової похибки підлягають однаковому закону розподілу і мають однакову довірчу ймовірність P, тоді і .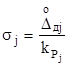

При нормальному законі розподілу всіх складових або при кількості складових n ³ 5 сумарна випадкова похибка має нормальний закон розподілу. Отже, її границі довірчого інтервалу з довірчою ймовірністю P можна визначити так: .