Дипломная работа: Аффинные преобразования евклидовой плоскости в сопряж нных комплексных координатах

Родство – аффинное преобразование, имеющее прямую неподвижных точек. Его задаёт формула :

, где ,, (20)

Осью этого преобразования является прямая , примем её за действительную ось Ох : [1]. Тогда очевидно, что с=0 и b =1- a . Поэтому преобразование (20) с действительной осью записывается формулой:

, где (21)

Рис. 2

Выясним особенности этого преобразования. Перепишем его следующим образом (22) составим из этого выражения и сопряжённого к нему выражения пропорцию . Откуда , а это является условием того, что векторы с координатами и перпендикулярны. Так как а-1 – постоянные вектор, а z и z ’ – координаты соответственных точек М и ̒ при аффинном преобразовании (рис. 2 ), то все прямые, соединяющие точки М и ̒ будут параллельны между собой и параллельны некоторому вектору с координатой (а-1) i , называемому направлением аффинного преобразования , в данном случае – родства.

Если (а-1) – чисто мнимое число (то есть , откуда ), то направление родства будет коллинеарно оси родства. В этом случае аффинное преобразование называется сдвигом вдоль прямой и условия, которые его задают, имеют вид , , (23)

Если же направление аффинного преобразования не совпадает с направлением его оси, то оно называется сжатием к прямой и его задают следующие условия: , , (24)

2.2. Сжатие и его частные виды

Найдём собственные числа λ преобразования сжатия (24) из условия . Составим систему из этого условия и сопряжённого к нему выражения : . Чтобы найти собственные числа, нужно решить уравнение , откуда получим и .

Примем без доказательства следующую теорему [1]: если λ – собственное действительное число аффинного преобразования, то множество точек, каждая из которых делит в отношении отрезок, соединяющий точку с её прообразом, есть двойная прямая этого преобразования.

Рис. 3

Очевидно, что прямые MM ’ и NN ’ (рис. 3 ) являются двойными прямыми и λ₂ – действительное число, то точка Р делит отрезок MM ’ в отношении , то есть . Число =δ называется коэффициентом сжатия . Если а – действительное число, то направление сжатия перпендикулярно его оси и сжатие называется прямым (ортогональным) сжатием .

Рассмотрим частный случай сжатия – косую симметрию [1]. Это инволютивное преобразование, то есть оно тождественно преобразованию, обратному ему. Преобразование, обратное (24), имеет формулу:

(25)

Оно имеет ту же ось, что и (24). Равенство преобразований (24) и (25) имеет место тогда и только тогда, когда , откуда , то есть а – чисто мнимое число. Таким образом, формулой (24) при условии задаётся косая симметрия с действительной осью. В этом случае коэффициент сжатия равен , следовательно, ось косой симметрии делит пополам каждый отрезок, соединяющий соответственные точки. Косая симметрия – аффинное преобразование второго рода, так как его определитель отрицателен.

Если а=0 , получаем осевую симметрию относительно действительной оси. Осевая симметрия – аффинное преобразование также второго рода ().

2.3. Сдвиг

Выясним, как перемещается по плоскости точка при сдвиге (рис.4 ). Рассмотрим равенство (22), возьмём модули обеих частей этого равенства

(26)

и посмотрим, чем является каждый модуль в (26).

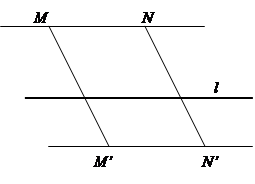Рис. 4

- это расстояние от точки М( z ) до её образа M ’( z ’) при аффинном преобразовании.