Дипломная работа: Алгоритмы с многочленами

kof2[i]:=k1_1[i];

end;

st3:=st1;

st1:=st2;

st2:=st3;

end;

end;

end.

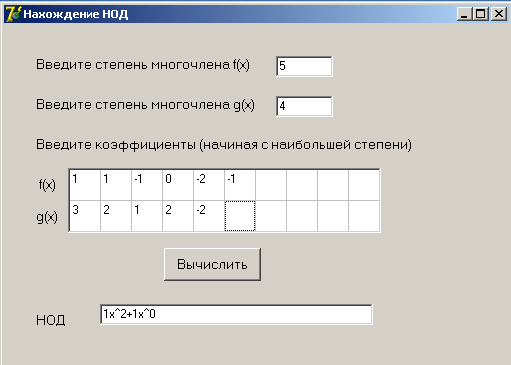
Используем алгоритм Евклида для доказательства следующей теоремы:

Теорема. Если есть наибольший общий делитель многочленов и , то можно найти такие многочлены и , что

. (2.5)

Можно считать при этом, если степени многочленов и больше нуля, что степень меньше степени , а степень меньше степени .

Доказательство основано на равенствах (2.4). Если учтем, что , и положим , , то предпоследнее из равенств (2.4) даст:

.

Подставляя сюда выражение через и из предшествующего равенства (2.4), получим:

,

где , . Продолжая подниматься вверх по равенствам (2.4), придем к доказываемому равенству (2.5).

Для доказательства второго утверждения теоремы предположим, что многочлены и , удовлетворяющие равенству (2.5), уже найдены, но, например, степень больше или равна степени . Делим на :

,

где степень меньше степени , и подставляем это выражение в (2). Получим равенство:

.

Степень множителя, стоящего при , уже меньше степени . Степень многочлена, стоящего в квадратных скобках, будет в свою очередь меньше степени , так как в противном случае степень второго слагаемого левой части была бы не меньше степени , а так как степень первого слагаемого меньше степени этого произведения, то вся левая часть имела бы степень, большую или равную степени , тогда как многочлен заведомо имеет, при наших предположениях, меньшую степень.

Теорема доказана.

Одновременно получаем, что если многочлены и имеют рациональные или действительные коэффициенты, то и многочлены и , удовлетворяющие равенству (2.5), можно подобрать так, что их коэффициенты будут рациональными или, соответственно действительными.

Применяя доказанную теорему к взаимно простым многочленам, получаем такой результат:

Многочлены и тогда и только тогда взаимно просты, если можно найти многочлены и , удовлетворяющие равенству