Дипломная работа: Экспериментальное исследование параметров плазы емкостного высокочастотного разряда (ЕВЧР)

Система уравнений для определения параметров разряда

Рассмотрим описанную выше картину, пользуясь уравнениями движения электронов в поле и электростатики. Обозначим через d₁ и d₂ мгновенные толщины левого и правого слоев. В отсутствие токов зарядов на электроды суммарные заряд и толщина двух слоев остаются неизменными:

en₊ d₁ + en₊ d₂ = const, иd₁ + d₂ = 2A (3)

Согласно (1) поля в левом (Е₁ ) и правом (Е₂ ) слоях распределены как

Е₁ = Е_р – 4πen(d₁ – x), E₂ = E_p + 4πen [x– (L – d₂ )] (4)

Потенциалы плазмы относительно левого и правого электродов, т.е. мгновенное падение напряжения в слоях, равны

V₁ = 2πend₁ ² , V₂ = 2πend₂ ² (5)

E_p = V/L + 8πen (A/L) y, y = d₁ – A(6)

Оно параметрическим образом связывает Е_р со смещением у левой границы плазмы (равным также смещению любого электрона из среднего положения). С другой стороны, смещение подчиняется общему уравнению движения электрона. При этом υ = y^’’ , а под Е_а sinωtследует подразумевать поле в плазме Е_р . Подставляя в общее уравнение движения электрона поле Е_р, взятое из (6), и используя выражение

ω_р = 5,64*10⁴ (n_e )^1/2 c^-1 (7)

для плазменной частоты, получаем уравнение для смещения электронов плазмы:

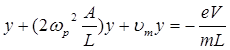(8)

Дальше удобнее оперировать гармоническими величинами в комплексной форме. Пусть к электродам приложено напряжение V=V_a e^iωt .Установившееся решение уравнения (8) есть

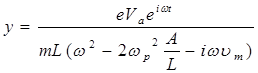(9)

Приравнивая действительную амплитуду смещения у величине A,которой она равна по определению, имеем

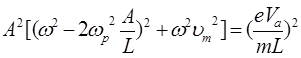(10)

Это – алгебраическое уравнение четвертой степени относительно A.Корень уравнения, который имеет физический смысл, определяет амплитуду колебаний электронов в зависимости от амплитуды напряжений V_а , частоты ω и плотности плазмы п. Последняя входит в (10) через ω_р в виде неизвестного пока параметра.

Как известно плотность плазмы связана с амплитудой поля в ней Е_р , ауравнением баланса числа зарядов, например условием ионизационно-рекомбинационного равновесия (11):

υ_{i ,ВЧ} (Е_а ) = υ_рек = βn(11)

Согласно (6) поле в плазме

(12)

Тем самым замыкается система уравнений модели, определяющая все параметры разряда. Уравнения (10) и (11) с амплитудой Е_{р, а} , определенной из (12), образуют систему двух уравнений длянахождения А и п в зависимости от приложенного напряжения (V_а и ω). Зная их, можно вычислить любые другие величины, например ток и импеданс разряда, а также построить ВАХ.

Разрядный ток

Плотность разрядного тока, т.е. тока, текущего во внешней цепи и, в частности, через электроды, по определению равна скорости изменения плотности поверхностного заряда q на левом электроде (с учетом выбранного направления оси х) .Электрод можно считать идеальным проводником. Поля, а потому и тока смещения Е/4πв нем нет. Плотность отрицательного заряда qна электроде совпадала бы по модулю с количеством положительного заряда в левом слое на единице площади end₁ , если бы плазма была также идеальным проводником. В плазме имеется весьма заметное поле E_р , которое призвано поддерживать ток и, возможно, состояние ионизации. Согласно законам электростатики оно связано с плотностями поверхностного заряда равенством

(13)

Дифференцируя равенство (13) по времени, находим плотность разрядного тока в видe

(14)

Величина j не зависит от х, будучи одинаковой, во всех сечениях разрядного промежутка. Первое слагаемое представляет собой плотность тока электронов (проводимости плюс поляризации), второе – «чистый» ток смещения. Появление последнего в выражении для сохраняющейся величины j – следствие несовершенства проводящих свойств плазмы. Именно по этой причине заряд в слое отличается по модулю от q, не успевая мгновенно реагировать на изменение заряда на электроде, который поступает из внешней цепи (или уходит во внешнюю цепь) под действием ЭДС источника питания. Подставив в (14) Е_р из (6), придадим выражению для плотности тока вид

(15)