Дипломная работа: Финансовые функции и рекурсия
revise(S,p,n) =invest(S,p,n),
и это соотношение может служить базой рекурсии. Декомпозицию реализуем, исходя из следующих соображений. Пусть length(n) >1 и задача 4 решена для векторов n1 и p1, полученных отбрасыванием последнего компонента соответственно у векторов n и p. Образовавшийся при этом новый размер вклада обозначим через sum. Тогда для получения решения исходной задачи с векторами n и p остается подсчитать сумму, возвращаемую при инвестировании величины sum на последние nk-1 периодов под pk-1 процентов. Иными словами, необходимо еще раз решить задачу 1, то есть вычислить значение функции invest(sum,pk-1,nk-1). Именно эти соображения и использованы при написании функции revise():

Рекурсивная функция revise1(S,p,n) построена на способе декомпозиции, вытекающем из таких соображений. Если исходную сумму S инвестировать под p0 процентов на n0 периодов, то с полученной суммой останется решить исходную задачу для векторов n и pc удаленными первыми компонентами:

Замечание. При необходимости можно было бы вывести конечную формулу для решения задачи 4. Выглядит она так:
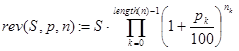
Контрольные примеры.
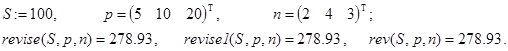
Задача о изменяющихся процентных ставках и величинах снимаемых денег
Вкладчик положил в сбербанк sum денежных единиц под pk (k=0. . n-1) процентов за каждый из n последующих периодов времени. В конце каждого периода k (k=0. . n-1) после начисления pk процентов он снимает со счета Ak денежных единиц. Иными словами, допускается, вообще говоря, и изменение процентной ставки, и величины денежных единиц, снимаемых с вклада. Составить программы, отвечающие на следующие вопросы:
Имеет ли задача решение?
Если задача имеет решение, то какова величина вклада после n периодов?
Если задача не имеет решения, то каков наименьший номер периода, в котором взятие соответствующей суммы оказалось невозможным?
Решение. Рассмотрим векторы процентных ставок и величин уменьшения вклада:
p=(p0,p1,…,pn-1) T, A=(A0,A1,…,An-1) T.
Ответ на первые два вопроса дают рекурсивные программы-функции waste2(sum,p,A) и waste3(sum,p,A). Если задача имеет решение, то они возвращают величину вклада после n периодов, а иначе - отрицательное число. Декомпозиция для функции waste2() проводилась, исходя из того же утверждения, что и для функции waste(), а декомпозиция для функции waste3() - исходя из того же утверждения, что и для функции waste1(). Во втором случае получена более компактная и ясная программа:
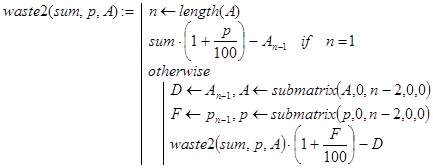
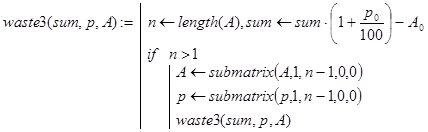
Наряду с этими программами можно вывести и конечную формулу wa(S,p,A) для расчетов. Пусть n=length(p). Тогда:
![]()
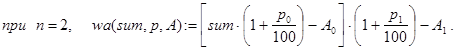
И, наконец, в общем случае:
![]()
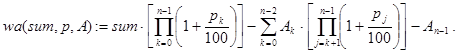
Контрольные примеры.
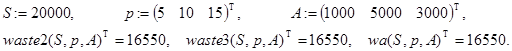
Попробуем теперь составить программу, отвечающую на третий из поставленных вопросов. Будем считать, что она должна возвращать вектор с двумя компонентами, который выглядит так:
[“O’key” решение] T, если задача имеет решение;
[период сальдо] T, если задача не имеет решения.