Дипломная работа: Финансовые функции и рекурсия

Платежи проводятся через m2 периодов. В (20) вместо k и p необходимо подставить соответственно значения k/m2 и p×m2.

Указанное замечание касается и многих других ранее рассмотренных функций.

Задача о равных платежах в конце или начале каждого периода.

Банк выдал заемщику кредит в pv денежных единиц на nper периодов с необходимостью выплаты долга равными частями в конце (type=0) или начале (type=1) каждого периода. Определить величину pmt разовых выплат, если процентная ставка банка за один период равна rate.

Решение. Данная задача может быть решена с помощью встроенной в Excel функции pmt=pmt(rate,nper,pv,type). При type=0 задачи 10 и 11 идентичны. Ниже приведено решение для общего случая, основанное на легко получаемой рекуррентной формуле. Будем исходить из того, что современная стоимость всех внесенных платежей должна быть равной произведенному займу pv. Пусть через pmtn (n=1,2,…) обозначена ставка платежей при выплатах за n периодов. Найдем связь между pmtn и pmtn-1, исходя из баланса современной стоимости платежей при любом n. Пусть type=0. Тогда

Отсюда

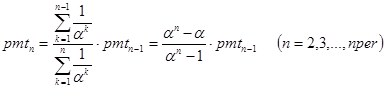(21)

То же самое соотношение получается и для type=1. Иными словами, при любом допустимом значении type имеет место следующая рекуррентная формула:

(22)

Раскрывая рекуррентность (22), получаем

(23)

(24)

Соотношения (24) и (22) и взяты соответственно в качестве базы и декомпозиции при реализации рекурсивной программы-функции pmt():

Из соотношений (23) и (24) при n=nper получается конечная формула для вычисления значений pmt():

Контрольные примеры.

Задача о платежах с одинаковой современной стоимостью

Некто занял pv денежных единиц на nper периодов при процентной ставке в rate процентов за период. Платежи ppmt по займу должны иметь одинаковую современную стоимость и производиться в конце (type=0) или начале (type=1) каждого периода. Определить величину платежа в период per (per=1,2,…,nper).

Решение. Данная задача может быть решена с помощью встроенной в Excel функции ppmt(rate,per,nper,pv,type). Получим её рекурсивную реализацию. Пусть pk (k=1,2,…,nper) - последовательные платежи.

Ра