Дипломная работа: Явление сверхпроводимости

Причём мы будем также пренебрегать разницей между частной и полной производными по времени. Предполагая, что токи создаются движением только сверхпроводящих электронов, напишем далее , где - концентрация таких электронов. После дифференцирования по времени получим . Ускорение электрона найдётся из уравнения , если пренебречь действием магнитного поля. Тогда

, (5)

где введено обозначение

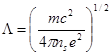. (6)

Продифференцировав первое уравнение (4) по , исключив из уравнений (4) и (5) величины и , получим

. (7)

Этому уравнению удовлетворяет , но такое решение не согласуется с эффектом Мейснера, так как внутри сверхпроводника должно быть . Лишнее решение получилось потому, что при выводе дважды применялась операция дифференцирования по времени. Чтобы автоматически исключить это решение, Лондоны ввели гипотезу, что в последнем уравнении производную следует заменить самим вектором . Это даёт

. (8)

Для определения глубины проникновения магнитного поля внутрь сверхпроводника допустим, что последний ограничен плоскостью по одну сторону от неё. Направим ось внутрь сверхпроводника нормально к его границе. Пусть магнитное поле параллельно оси , так что . Тогда

, (9)

И уравнение (8) даёт

. (10)

Решение этого уравнения, обращающееся в нуль при , имеет вид

.

Постоянная интегрирования даёт поле на поверхности сверхпроводника. На протяжении длины магнитное поле убывает в раз. Величина принимается за меру глубины проникновения поля в металл.

Для получения численной оценки примем, что на каждый атом металла приходится один сверхпроводящий электрон, полагая см^-3 . тогда по формуле (6) найдём см, что по порядку величины совпадает со значениями, полученными непосредственными измерениями.

Поверхностный слой сверхпроводника обладает особыми свойствами, связанными с отличной от нуля напряженностью магнитного поля в нем. Эти свойства оказывают очень существенное влияние на получение сверхпроводников с высокими критическими полями.

Возникает ситуация, когда поверхностные токи, часто называемые экранирующими, препятствуют проникновению в образец магнитного потока приложенного поля. Если внутри вещества, находящегося во внешнем поле, магнитный поток равен нулю, то говорят, что он проявляет идеальный диамагнетизм. При снижении плотности приложенного поля до нуля образец остается в своем ненамагниченном состоянии. В другом случае, когда магнитное поле приложено к образцу, находящемуся выше переходной температуры, конечная картина заметно изменится. Для большинства металлов (кроме ферромагнетиков) значение относительной магнитной проницаемости близко к единице. Поэтому плотность магнитного потока внутри образца практически равна плотности потока приложенного поля. Исчезновение электросопротивления после охлаждения не оказывает влияния на намагниченность, и распределение магнитного потока не меняется. Если теперь снизить приложенное поле до нуля, то плотность магнитного потока внутри сверхпроводника не может меняться, на поверхности образца возникают незатухающие токи, поддерживающие внутри магнитный поток. В результате образец остается все время намагниченным. Таким образом, намагниченность идеального проводника зависит от последовательности изменения внешних условий.

Эффект выталкивания магнитного поля из сверхпроводника можно пояснить на основе представлений о намагниченности. Если экранирующие токи, полностью компенсирующие внешнее магнитное поле, сообщают образцу магнитный момент m, то намагниченность M выражается соотношением:

, (11)

где V - объем образца. Можно говорить о том, что экранирующие токи приводят к появлению намагниченности, соответствующей намагниченности идеального ферромагнетика с магнитной восприимчивостью, равной минус единице.

Эффект Мейсснера и явление сверхпроводимости тесно связаны между собой и являются следствием общей закономерности, которую и установила созданная более чем через полвека после открытия явления теория сверхпроводимости.

1.4 Изотопический эффект

В 1950 г. Е. Максвелл и Ч. Рейнольдс открыли изотопический эффект, который имел большое значение для создания современной теории сверхпроводимости. Исследование нескольких сверхпроводящих изотопов ртути показало, что существует связь между критической температурой перехода в сверхпроводящее состояние и массой изотопов. При изменении массы М изотопа от 199,5 до 203,4 критическая температура изменялась от 4,185 до 4,14 К. Для данного сверхпроводящего химического элемента была установлена формула, оправдывающаяся с достаточной точностью:

, (12)

где const имеет определённое значение для каждого элемента.

Масса изотопа является характеристикой кристаллической решётки, так как в неё основной вклад вносят ионы металла. Масса определяет многие свойства решётки. Известно, что частота ω колебаний решётки связана с массой:

. (13)

Сверхпроводимость, которая является свойством электронной системы металла, оказывается связанной, ввиду обнаружения изотопического эффекта, с состоянием кристаллической решетки. Следовательно, возникновение эффекта сверхпроводимости обусловлено взаимодействием электронов с решеткой металла. Это взаимодействие ответственно за сопротивление металла в обычном состоянии. При определенных условиях оно должно приводить к исчезновению сопротивления, то есть к эффекту сверхпроводимости.