Дипломная работа: Инверсия и ее применение

Если окружность г касается базисной окружности щ, то г преобразуется в общую касательную этих окружностей.

Если две окружности касаются в центре инверсии, то они преобразуются при инверсии в пару параллельных прямых.

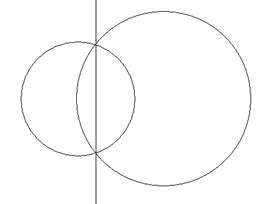
Рис. 20

Теорема. При инверсии окружность, не проходящая через центр инверсии, преобразуется в окружность.

Доказательство. Пусть щ (О, r) – базисная окружность (рис. 21), г (О1, r1) – данная окружность. Проведем прямую ОО1 и отметим точки А и В ее пересечения с окружностью г. Пусть Аґ и Вґ - инверсные им точки. Обозначим через Р произвольную точку окружности г, через Рґ - инверсную ей точку. Соединим Р с А и В, Рґ с Аґ и Вґ. из леммы об антипараллельных прямых вытекает, что ∟1′ = ∟1, ∟2′ = ∟2. Но ∟1 + ∟2 = 90є. Поэтому ∟1ґ + ∟2ґ = 90є. Следовательно, ∟АґРґВґ = 90є. Таким образом, из точки Рґ отрезок АґВґ виден под прямым углом. Значит, точка Рґ лежит на окружности с диаметром АґВґ. Обозначим эту окружность через гґ. Мы доказали, что каждая точка окружности г при инверсии преобразуется в точку окружности гґ.

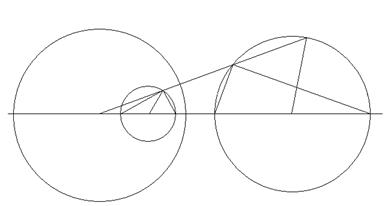
Рис. 21

По ходу доказательства теоремы выясняется следующий способ построения окружности, инверсной данной окружности (если последняя не проходит через центр инверсии): 1) проводим прямую через центр инверсии О и центр О1 данной окружности г; 2) отмечаем точки А и В пересечения этой прямой с окружностью гґ; 3) строим инверсные точки Аґ и Вґ; 4) строим окружность гґ на отрезке АґВґ как на диаметре. Окружность гґ искомая.

1.6 Преобразование прямой при инверсии

При инверсии прямая, проходящая через центр инверсии, преобразуется сама в себя. Как обстоит дело с прямой, не проходящей через центр инверсии?

Теорема. При инверсии прямая, не проходящая через центр инверсии, преобразуется в окружность, проходящую через центр инверсии.

Доказательство. Пусть щ (О, r) – базисная окружность (рис. 22), а – данная прямая. Опустим из точки О перпендикуляр ОА на прямую а. Пусть Аґ - точка, инверсная точке А, а г – окружность, имеющая диаметром ОАґ.

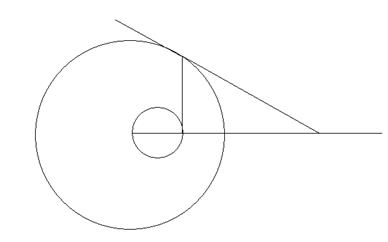
Рис. 22

При инверсии окружность г преобразуется в прямую а (по теореме из пункта 1.5). в силу свойства взаимности прямая а преобразуется в окружность г.

Заметим, что по ходу доказательства мы выяснили способ построения окружности, инверсной данной прямой.

1.7 Инвариантные окружности. Сохранение углов при инверсии

При инверсии базисная окружность преобразуется в себя. Но существуют и другие окружности, обладающие таким свойством.

Вспомним некоторые определения.

Углом между двумя линиями в точке их пересечения Т называется угол между касательными к этим линиям, проведенным в точке Т.

Две окружности называются ортогональными, если они пересекаются под прямым углом. Если две окружности ортогональны, то их радиусы, проведенные в точку пересечения, перпендикулярны между собой, и наоборот.

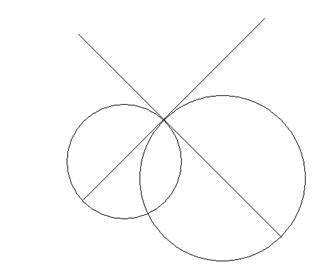
Рис. 23

Отсюда вытекает способ построения окружностей, ортогональных данной окружности щ в данной точке Т. для этого достаточно на касательной t к окружности щ в точке Т выбрать произвольную точку О1 и построить окружность щ1 (О1, О1Т), которая и будет искомой (рис. 23).

Теорема. Для того чтобы окружность, отличная от базисной окружности, преобразовалась при инверсии в себя, необходимо и достаточно, чтобы она была ортогональна базисной окружности.

Доказательство. 1) Достаточность. Пусть окружность г (О1, r1) (рис. 24) ортогональна базисной окружности щ (О, r). Докажем, что окружность г преобразуется в себя.

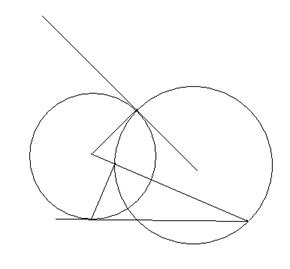
Рис. 24