Дипломная работа: Исследование фазовых эффектов в бинарных азеотропных смесях

dgж= -Sж dT +Vж dР+ μ1dх1+ μ2 dх2 2.8

Аналогично для паровой фазы имеем

Sп dT –Vп dР+ у1 dμ1 + у2 dμ2=0 2.9

dgп= -Sп dT +Vп dР+ μ1dу1+ μ2 dу2 2.10

В работе [14] дан вывод нулевого потенциала. Приведем его полностью. Для случая бинарной смеси уравнение внутренней энергии имеет вид:

U= TS-PV+ μ1x1+ μ2x2 2.11

После дифференцирования получаем

dU= TdS + SdT – PdV – VdP + μ1 dx1 + x1dμ1 + μ2 dx2 + x2dμ2 2.12

Но так как

dU= TdS - PdV+ μ1 dx1 + μ2 dx2 2.13

то очевидно

SdT-VdP+ x1dμ1+ x2dμ2 =0 2.14 Если применять почленно преобразование Лежандра, то, учитывая, что при этом меняется в каждом случае знак, получим

-SdT+VdP- x1dμ1- x2dμ2 =0 2.15

Автор [14] не видит разницы между уравнениями в форме 2.14 и 2.15, поэтому приводит уравнение 2.15, очевидно считая, что если правая часть равна нулю, то обе формы идентичны.

Как уже говорилось, нулевой потенциал есть скалярное произведение вектора

< S, V, x1, x2 >

на вектор < dT, dP, dμ1, dμ2 >

Учитывая, что это скалярное произведение равно нулю, векторы-сомножители ортогональны друг другу.

Так как, вектор < dT, dP, dμ1, dμ2 > есть вектор параметров, которые могут изменяться независимо, очевидно вектор < S, V, x1, x2 > может быть представлен двояко < S, -V, x1, x2 > или <- S, V, -x1, - x2 >

Оба представления получаются равнозначными, так как эти векторы ортогональны. Проиллюстрируем это при условии Р=соnst. В этом случае имеем

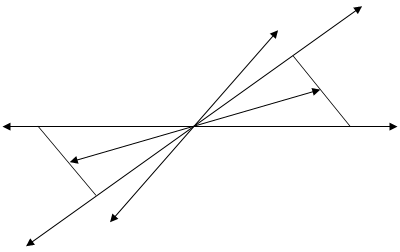< S, x1, x2 > и <- S, -x1, - x2 > S

S х1 х2 х1

х

-х2 х2

-х

-S -х1 -х2

-х1

- S

Рис.2.10. Взаимное расположение вектора состава