Дипломная работа: Исследование магнитных систем в программной системе конечно-элементного анализа ANSYS
![]()

Рис. 2.4 Технические требования для расчета силы магнитного поля на исследуемый объект в программной системе конечно-элементного анализа ANSYS.
В таблице 2.1 приведены результаты расчета силы магнитного поля на верхний магнит с помощью программной системы конечно-элементного анализа ANSYS.
Таблица 2.1 Зависимость силы, действующей на верхний магнит от воздушного зазора между магнитами.
| № | Воздушный зазор, мм. | Метод расчета силы с помощью виртуальной работы, N | Метод расчета силы с помощью тензора напряжений Максвелла, N |
| 1 | 1 | 4,61 | 4,51 |
| 2 | 2 | 3,11 | 3,12 |
| 3 | 3 | 2,20 | 2,20 |
| 4 | 4 | 1,63 | 1,61 |
| 5 | 5 | 1,22 | 1,20 |
| 6 | 6 | 0,91 | 0,90 |
| 7 | 7 | 0,69 | 0,67 |
| 8 | 8 | 0,53 | 0,52 |
| 9 | 9 | 0,42 | 0,41 |
| 10 | 10 | 0,33 | 0,33 |
| 11 | 12 | 0,22 | 0,21 |
| 12 | 14 | 0,15 | 0,14 |
| 13 | 17 | 0,09 | 0,08 |

Рис.2.5 Зависимость силы магнитного поля, действующего на верхний магнит от величины воздушного зазора.
2.1.4 Исследование сходимости методов расчета силы магнитного поля в зависимости от величина воздушного пространства, окружающего магнитную систему
Была исследована сходимость методов расчета силы магнитного поля в зависимости от величины воздушного пространства, окружающего магнитную систему. Выбор оптимального воздушного пространства позволяет корректно использовать “потокопараллельное” граничное условие, и не перегружать программную систему конечно-элементного анализа ANSYS лишними расчетами.
Таблица 2.2 Анализ сходимости методов расчета силы магнитного поля на верхний магнит в зависимости от величина воздушного пространства, окружающего магнитную систему.
| № | Ширина модели воздушного слоя, окружающего магнитную систему, мм | Метод расчета силы с помощью виртуальной работы, N | Метод расчета силы помощью тензора напряжений Максвелла, N | Отклонение текущего значения к последнему (метод виртуальной работы) % | Отклонение текущего значения к последнему (Метод расчета с помощью тензора Максвелла) % |
| 1 | 5 | 1,8415 | 1,8114 | 26,60422 | 26,51223 |
| 2 | 8 | 2,213 | 2,1755 | 11,79753 | 11,74084 |
| 3 | 10 | 2,3146 | 2,275 | 7,74811 | 7,70417 |
| 4 | 30 | 2,487 | 2,4436 | 0,87684 | 0,86413 |
| 5 | 50 | 2,503 | 2,4591 | 0,23914 | 0,2353 |
| 6 | 70 | 2,5072 | 2,4632 | 0,07174 | 0,06897 |
| 7 | 100 | 2,509 | 2,4649 |

Рис.2.6 Зависимость силы магнитного поля, действующей на верхний магнит, от величины воздушного пространства, окружающего магнитную систему.
Из таблицы 2.2 и рис. 2.6 видно, что уже при ширине равной 30 мм воздушного пространства, окружающего магнитную систему. отклонение текущего значения к последнему меньше 1%. Поэтому в исследуемой модели ширина воздушного слоя выбирается равной 40мм, это в 8 раз больше радиуса постоянного магнита.
2.1.5 Исследование сходимости методов расчета силы магнитного поля в зависимости от количества элементов модели
Была исследована сходимость методов расчета силы магнитного поля в зависимости от количества элементов модели. Важно отметить, что точность вычислений существенно зависит от числа элементов модели.
Таблица №2.3 Анализ сходимости методов расчета силы магнитного поля на верхний магнит.
| № | Количество элементов модели | Метод расчета силы с помощью виртуальной работы, N | Метод расчета силы помощью тензора напряжений Максвелла, N | Отклонение текущего значения к последнему (метод виртуальной работы) % | Отклонение текущего значения к последнему (Метод расчета с помощью тензора Максвелла) % | Отклонение Текущего значения, полученного методом расчета с помощью тензора Максвелла от текущего значения, полученного методом виртуальной работы, % |
| 1 | 50 | 1,4732 | 0,3913 | 8,07 | 75,11 | 73,44 |
| 2 | 60 | 1,4740 | 0,3923 | 8,02 | 75,04 | 73,39 |
| 3 | 96 | 1,5177 | 0,3831 | 5,30 | 75,63 | 74,76 |
| 4 | 112 | 1,5589 | 0,5774 | 2,73 | 63,27 | 62,96 |
| 5 | 280 | 1,5832 | 1,2676 | 1,21 | 19,36 | 19,93 |
| 6 | 1000 | 1,5920 | 1,3496 | 0,66 | 14,15 | 15,23 |
| 7 | 8100 | 1,6038 | 1,5359 | -0,07 | 2,30 | 4,23 |
| 8 | 12120 | 1,6019 | 1,5500 | 0,04 | 1,40 | 3,24 |
| 9 | 20400 | 1,6026 | 1,5720 | 0,00 | 0,00 | 1,91 |

Рис. 2.7 Зависимость силы магнитного поля, действующей на верхний магнит, от количества элементов модели.

Рис.2.8 Отклонение текущей величины силы магнитного поля, действующей на верхний магнит от наилучшей последней величины в зависимости от количества элементов сетки модели.
Из рисунка 2.8 видно, что для метода расчета с помощью виртуальной работы, даже при грубой сетке в 50 элементов, сила магнитного поля, действующая на верхний магнит, дает отклонение не более 10% от значения, полученного для модели с сеткой в 20400 элементов. Рис.2.9. Для метода расчета с помощью Тензора Напряжений Максвелла отклонение значений силы магнитного поля, меняется в значительно более широком диапазоне от 75% до 1.4%, в зависимости от грубости сетки модели. Т.е. метод расчета с помощью виртуальной работы сходится быстрее, и требует намного меньше времени и ресурсов счета программой.

Рис.2.9 Вид созданной КЭ модели, воздушный зазор между магнитами 4мм, сетка модели 50 элементов.
2.1.6 Расчет силы магнитного поля на верхний магнит устройства методами программной системы конечно-элементного анализа ANSYS с использованием элементов, моделирующих затухание поля в дальней зоне. Сравнение результатов
Выше исследовалась модель с “потокопараллельным” граничным условием, которое подразумевало, что поток не будет выходить за внешние границы модели и будет параллелен им. Рассмотрим альтернативный вариант граничного условия: использование элементов не ограничивающих модель. На границе области зададим затухание магнитного поля в дальней зоне с помощью слоя элементов Infin110. Infin110 – восьмиузловой элемент, в каждом узле он имеет одну степень свободы z-составляющую магнитного векторного потенциала Az.
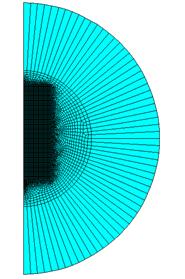
Рис.2.10 Вид созданной КЭ модели, воздушный зазор между магнитами 4мм.
Данная модель имеет 24019 узлов и 7920 элементов, обладает 24019 степенями свободы.
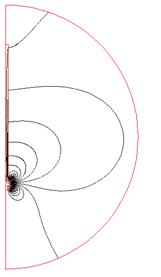
Рис.2.11 Эквипотенциальные линии магнитной индукции при величине воздушного зазора между постоянными магнитами равного 4мм.