Дипломная работа: Исследование магнитных систем в программной системе конечно-элементного анализа ANSYS
Была рассчитана сила магнитного поля на нижний магнит модели. Сравнение результатов, с полученными ранее для модели с “потокопараллельным” граничным условием, приведено в таблице 2.4.
Таблица 2.4. Сравнение результатов расчета силы магнитного поля на нижний магнит для модели с воздушны зазором между магнитами 4мм.
| № | Метод расчета силы магнитного поля на нижний магнит модели. | Модель с “потокопараллельным” граничным условием, N | Модель с использованием элементов Infin, N | Отклонение результата модели с “потокопараллельным” граничным условием от модели с использованием элементов Infin, % |
| 1 | Virtual Work | 1.6044 | 1.6026 | 0.11 |
| 2 | Maxwell Stress Tensor | 1.4810 | 1.5720 | 5,79 |
По результатам таблицы 2.4 видно, что для метода виртуальной работы отклонения результата несущественно. Для метода расчета с помощью тензора напряжений Максвелла результаты хуже на 5.79%. Т.е для расчетов задач такого рода можно пользоваться обоими способами задания граничных условий.
2.1.7 Расчет магнитостатического трехмерного поля в кусочно-однородной трехмерной области. Расчет силы магнитного поля на нижний магнит устройства. Сравнение результатов
2.1.7.1 Стратегии решения задачи
Наилучшее приближение численного решения к параметрам реального устройства можно получить при помощи трехмерного моделирования, в котором учитываются все три пространственные координаты. В пакете Ansys реализованы алгоритмы для двух формулировок электромагнитных задач: векторной (Magnetic Vector Potential - MVP) и скалярной (Magnetic Scalar Potential - MSP).
Как отмечается в документации по пакету, метод магнитного векторного потенциала в сравнении с методом скалярного потенциала более труден в реализации модели, а также дает меньшую точность в моделях, содержащих области с различной магнитной проницаемостью.
Метод MVP реализуется при помощи КЭ типа SOLID97, при этом области тока являются частью конечно-элементной модели, и их параметры задаются как константы (Real Constants) соответствующих КЭ. Метод MSP реализуется при помощи КЭ типа SOLID96 и SOLID98, при этом области тока не являются частью конечно-элементной модели, а задаются специальными КЭ типа SOURC36, геометрическое пространство которых может пересекаться с пространством конечно-элементной сетки модели. Для этого случая в пакете существует макрос, при помощи которого можно легко задать катушку
намагничивания.
Для решения задач на основе скалярного магнитного потенциала в пакете ANSYS используются три стратегии:
1) Reduced Scalar Potential (RSP) Strategy – стратегия упрощённого скалярного потенциала;
2) Difference Scalar Potential (DSP) Strategy - стратегия разностного скалярного потенциала;
3) General Scalar Potential (GSP) Strategy - стратегия обобщённого скалярного потенциала.
Их различие состоит в некоторых упрощениях уравнений моделирующих поле. Стратегия решения задаётся пользователем на этапе решения. От её выбора зависит правильность результатов расчёта. [1]
2.1.7.2 Расчёт трёхмерной магнитостатической задачи на примере исследуемой установки .
Проводится расчет магнитостатического трехмерного поля для кусочно-однородной, линейной изотропной (абсолютная магнитная проницаемость µ = 1) среды моделирования исследуемой магнитной системы. Модель устройства приведена на рис. 2.12. Стальной стержень и постоянные магниты расположены в воздушной среде. Для разбиения модели устройства регулярной сеткой воздушная среда моделируется сплошным цилиндром.
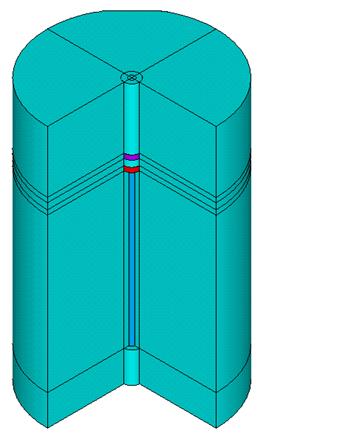
Рис. 2.12 Модель устройства магнитной пружины.
Для создания КЭ модели используется элемент Solid96 – восьмиузловой элемент. В каждом узле он имеет одну степень свободы – суммарную составляющую электромагнитного потенциала. Вид созданной КЭ модели приведен на рис.2.13 при величине воздушного зазора равного 4 мм.
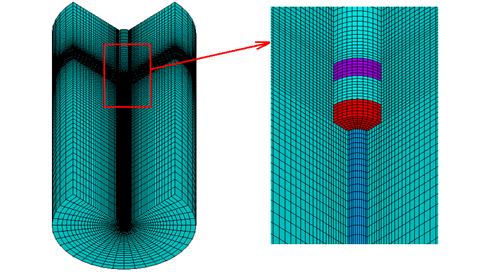
Рис. 2.13 Вид созданной КЭ модели магнитной пружины, воздушный зазор между магнитами 4мм.
Данная модель имеет 41561 узел и 13600 элементов, обладает 41561 степенью свободы.
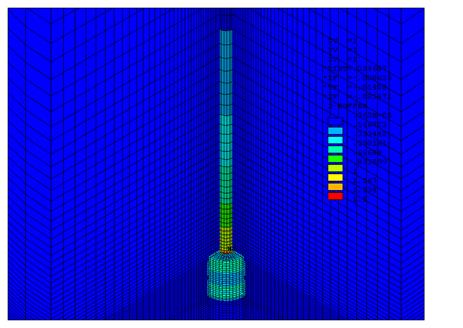
Рис.2.14 Распределение модуля вектора магнитной индукции (BSUM).
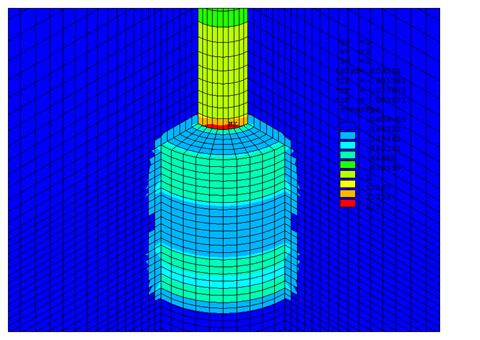
Рис.2.15 Распределение модуля вектора магнитной индукции (BSUM) вблизи системы постоянных магнитов.
Была рассчитана сила магнитного поля на нижний магнит модели. Сравнение результатов, с полученными ранее моделями приведено в таблице 2.5.
Таблица 2.5. Сравнение результатов расчета силы магнитного поля на нижний магнит для модели с воздушны зазором между магнитами 4мм.
| № | Метод расчета силы магнитного поля на нижний магнит модели. | Модель с “потокопараллельным” граничным условием, N |
Модель с использованием элементов Infin, К-во Просмотров: 329
Бесплатно скачать Дипломная работа: Исследование магнитных систем в программной системе конечно-элементного анализа ANSYS
|