Дипломная работа: Характеристика различных способов тригонометрического нивелирован

В первой предполагается равенство углов земной рефракции при одновременном изменении вертикальных углов на концах линии в направлении друг на друга.

Во второй – равенство углов земной рефракции при одновременных измерениях вертикальных углов с точки стояния инструмента в любых направлениях.

Первая гипотеза учитывает разнообразие условий рельефа по линиям, а вторая идентичность условий наблюдений в точке стояния инструментов.

Рассмотрим теорию различных способов тригонометрического нивелирования

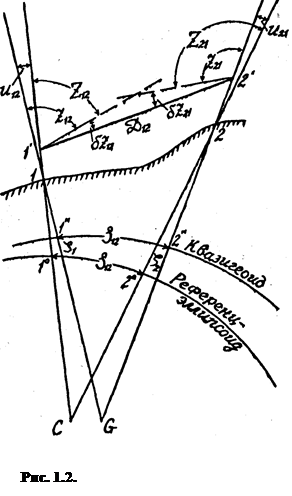
Геометрические построения для этого выполнены на рис. 1.2.

1', 2' места, установки теодолитов;

1,2 - центры знаков на земной поверхности;

1"2" - проекции точек 1 и 2 на поверхность квазигеоида;

1°,2° проекции точек 1 и 2 на поверхность референц-эллипсоида;

1С, 2С- нормали к поверхности референц-эллипсоида, проходящие через точки 1 и 2 соответственно;

1G, 2G - отвесные линии проходящие через точки 1 и 2;

Z₁₂ , Z₂₁ - зенитные расстояния точек 1 и 2, отнесенные к нормалям референц-эллипсоида в этих же точках;

z₁₂ , z₂₁ - измеренные в точках 1 и 2 зенитные расстояния;

δz₁₂ , δz₂₁ - величины углов земной рефракции в точках 1' и 2' по направлению 1-2.

На рис. 1.2 показано, что нормали и отвесные линии пересекаются в точке С и G. На самом деле этого не происходит, точки С и G надо рассматривать как пересечение проекций линий 1С, 2С, 1G, 2G, на плоскость чертежа, совпадающую с плоскостью нормального сечения с точки 1 на точку 2.

Для упрощения обозначим отрезок 11' представляющий высоту инструмента в точке 1 через i₁ , а 22' через i₂ . Примем, что высоты инструментов и визирных целей на этих точках равны между собой, то есть i₁ = l₁ и i₂ = l₂ .

Отрезки 11' и 22', характеризующие абсолютные отметки точек 1 и 2 в системе нормальных высот, обозначим через Н₁ и Н₂ соответственно.

Высоты точек 1 и 2 над поверхностью референц-эллипсоида равные 11° и 22° обозначим через Q₁ и Q₂ , а высоты квазигеоида над поверхностью референц-эллипсоида в этих же точках обозначим через ζ₁ и ζ₂ .

Проекцию линии 12, изображенную дугами 1°2° ≈ 1"2", на поверхности относимости обозначим через S . Длины этих дуг с точностью до малых величин третьего порядка относительно сжатия принятого эллипсоида можно считать равными длине дуги окружности с радиусом R, определяемым по формуле:

R = (1.7)

где N – радиус кривизны первого вертикала,

А₁₂ – азимут линии 12, а величина

η = e'cos² Bm

где e' – второй эксцентриситет эллипсоида,

Bm – средняя широт точек 1 и 2.

Значения высот по отвесным линиям и нормалям к референц-эллипсоиду можно принимать практически одинаковыми. Разница этих высот в самом неблагоприятном случае, при Н = 7 км, не превышает 0,2мм.

В системе нормальных высот для одностороннего тригонометрического нивелирования имеем:

h₁₂ = S ctg(z₁₂ + δz₁₂ ) + + i₁ – l₂ + (U₁₂ – U₂₁ )S + ΔЕ₁₂ (1.8)

а для двухстороннего: