Дипломная работа: Методика формирования умений решать тригонометрические уравнения и неравенства в курсе алгебры и начал анализа
Полезно помнить, что при
; 
;
.
Уравнение вида 
.
Если 
, то 
Если 
, то 
(рис 1, д)
Особые случаи:
; 
; 
; 
Нужно помнить, что при 
;
;
.
Уравнение вида 
.
(рис 1, и)
Нужно помнить, что при 
; 
;
Уравнение вида 
.
(рис 1, к)
Нужно помнить, что при 
; 
;
; 
Уравнения, сводящиеся к простейшим, имеют вид 
, 
, 
, 
.
Данные уравнения также являются простейшими и решаются сначала относительно f ( x ) , а затем полученные уравнения решаются относительно х.
Примеры:
1. 
;
2. 
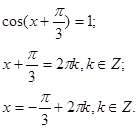
3. 
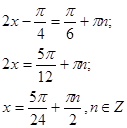
1.4.2 Уравнения, являющиеся равенством двух одноимённых тригонометрических функций: