Дипломная работа: Методика формирования умений решать тригонометрические уравнения и неравенства в курсе алгебры и начал анализа

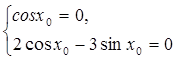, то .

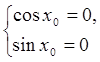Но это невозможно, т.к. .

Следовательно, имеем равносильное уравнение

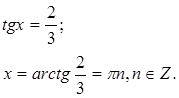
2. .

Это однородное уравнение второй степени. Получим равносильное уравнение после деления обеих частей уравнения на .

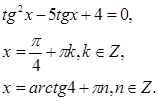[5, c.9]

1.4.5 Уравнения, решающиеся разложением на множители

При решении уравнений такого типа необходимо пользоваться известным правилом: произведение нескольких множителей равно нулю, если хотя бы один из них равен нулю, а остальные при этом имеют смысл.

Примеры:

1.

Используя данное правило получим:

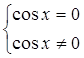или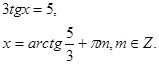

2.

Сгруппируем соответствующие слагаемые, получим:

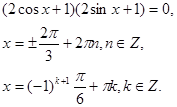
1.4.6 Уравнения вида

Один из способов решения такого уравнения состоит в том, что левую часть уравнения можно преобразовать по формуле:

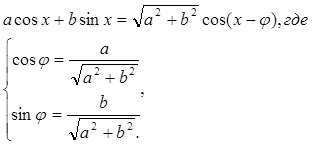
Примеры:

1.

;

, т.к. это решение системы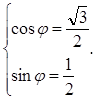

Подставляя в формулу, получаем:

2.

, т.к. это решение системы