Дипломная работа: Методика формирования умений решать тригонометрические уравнения и неравенства в курсе алгебры и начал анализа

б) уравнения вида равносильно системе уравнений:

в) уравнения вида равносильно системе уравнений:

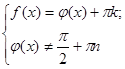
Примеры:

1. Решите уравнение:

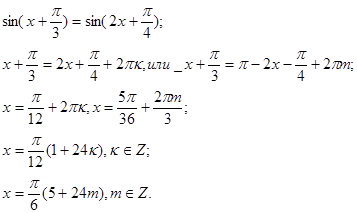
2. Решите уравнение:

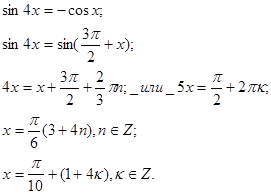
1.4.3 Тригонометрические уравнения, содержащие одну и ту же функцию одного и того же аргумента и решаемые методом подстановки

Уравнения данного вида , где тригонометрическая функция часто называются сводящимися к квадратным и решаются методом подстановки вместо тригонометрической функции данного аргумента некоторого параметра t с учётом допустимых значенийt в зависимости от области значения функции.

Пример: Решите уравнение:

Пусть тогда уравнение примет вид:

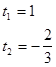
Оба корня уравнения удовлетворяют условию допустимого значения t , следовательно, переходим к обратной замене.

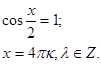
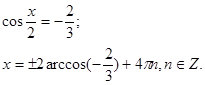[29]

1.4.4 Однородные уравнения

Предварительно можно показать учащимся вид однородной функции от двух переменных U и V первой степени, например, 3 U + 2 V ; второй степени: ; третьей степени: и т.д., сформировав понятия выражения, однородного относительно переменных U и V .

Для лучшего усвоения и закрепления идеи необходимо решить с учащимися следующее уравнение:

.

Обозначим

Получается однородное уравнение второй степени:

;

Имеем 2 случая: U = Vили V = 0,5 U

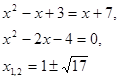
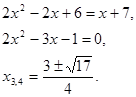
Как правило, на практике очень часто встречается .

Примеры:

1. .

Это однородное уравнение первой степени. Обе части уравнения нужно разделить на cosx . При этом получится равносильное уравнение. Чтобы в этом удостовериться, покажем, что уравнение cosx = 0 не содержит корней данного уравнения.