Дипломная работа: Методика оптимизации структуры и параметров библиотечной автоматизированной системы обеспечения информационными услугами

Тогда, если - последовательность значений случайной величины , равномерно распределенной в [0;1], то, решая уравнение (1.3), получим соответствующую последовательность случайных чисел, распределенных по закону (1.1), причем

(1.4)

Рассмотрим примеры.Пусть требуется получить случайные числа с показательным законом распределения

(1.5)

Используя (1.4), получим

(1.6)

где - случайная величина с равномерным распределением на интервале [0;1]. Отсюда

(1.7)

Тогда

(1.8)

Пусть теперь нужно получить случайные величины, распределенные по релеевскому закону с плотностью

(1.9)

Имеем

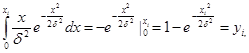(1.10)

Откуда

(1.11)

Нужно иметь в виду, что в большинстве случаев уравнение (1.3) невозможно решать точно (например, если требуется получить числа, распределенные по нормальному закону). В связи с этим на практике широко используют приближенные методы получения чисел, распределенных в соответствии с заданным законом. Рассмотрим один из таких алгоритмов.

1.2 Метод Неймана

Пусть - плотность распределения случайной величины, заданной на конечном интервале В предположении, что ограничена сверху, приведем ее значения к интервалу , введя

(1.12)

При этом график окажется вписанным в прямоугольник с координатами (a;0), (a;1), (b;1), (b;0), (рис. 1.1).

Рис. 1.1 - График

Выберем пару чисел и из равномерно распределенных в интервале последовательностей При этом пара чисел и определяет случайную точку в указанном прямоугольнике. Теперь в качестве случайных чисел с заданной плотностью будем принимать те , для которых Если же это неравенство не выполняется, то пара отбрасывается и формируется следующая.

Докажем, что закон распределения отобранных таким образом чисел соответствует распределению Для доказательства выберем интервал и введем области

и

(1.13)

Вычислим вероятность попадания не отброшенных точек в область Так как

(1.14)

а

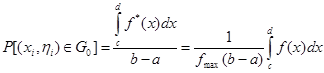(1.15)