Дипломная работа: Многоквантовые переходы под действием электромагнитного поля

1.1. Общие свойства многоквантовых переходов

К многоквантовым переходам, как известно, относятся переходы между электронными состояниями атомных, молекулярных или других систем, когда в одном элементарном акте происходит поглощение нескольких (более двух) квантов. Отдельным классом многоквантовых переходов являются многоквантовые переходы в двухуровневых системах, в которых проявляются эффекты квазипересечения адиабатических поверхностей. Именно этим задачам посвящена настоящая дипломная работа. В частности, в дипломной работе решается вопрос об отклонениях результатов расчетов вероятностей неадиабатических переходов от результатов стандартной теории возмущений и устанавливаются критерии применимости результатов теории возмущений. Теория ряда неадиабатических эффектов, появляющихся в многоквантовой спектроскопии молекул и твердых тел построена в работах [1, 7, 8]. Там решены некоторые задачи неадиабатических безизлучательных переходов. Весь комплекс задач, решенных в дипломной работе, связан с развитием современных представлений о воздействии сильного электромагнитного поля на вещество. Последнее, находится в фокусе интересов теоретических и экспериментальных исследований и свидетельствует об актуальности рассматриваемого в дипломной работе вопроса. Большинство решенных в дипломной работе задач основывается на асимптотических методах (метод ВКБ, метод перевала), которые применимы к задаче неадиабатического перехода с большим числом квантов, участвующих в переходе. Вычисление и построение графиков производилось с использованием пакета MathCAD версии 8.0.

Процессы поглощения и рассеяния света квантовыми системами в присутствии интенсивной когерентной волны хорошо изучены теоретически и экспериментально [1]. Статистические свойства внешнего электромагнитного поля существенно проявляются как в величине оптических сечений процессов для «пробного» излучения, так и в их частотной и интенсивностной зависимостях от параметров внешней лазерной волны. В последнее время большой интерес вызывает взаимодействие сжатого света с веществом, при котором могут проявляться неклассические свойства электромагнитного поля [3-4]. В литературе сообщается о возможностях создания интенсивных источников сжатого света, в том числе низкочастотных (микромазеры), что позволяет рассмотреть влияние фотонов этого излучения на сечение оптических процессов, при этом фотон пробного излучения напряженностью может намного превосходить фотон сжатого света с напряженностью F. Например, для двухуровневой атомарной или молекулярной системы с электронной щелью процесс поглощения частоты определяется законом

(1)

(k = 0, +1, …). Интенсивность комбинационного процесса поглощения света для k-го сателлита -света определяется через матричные элементы дипольного взаимодействия. Для обобщенной двухуровневой системы, имеющей ненулевой дипольный момент d в возбужденном электронном состоянии (2) и, для простоты, равный нулю дипольный момент в основном электронном состоянии (1), зависимость оптических сечений процессов от интенсивности сжатого света может носить немонотонный характер. Это обстоятельство проявляется в том, что корреляционных функций наиболее низкого порядка недостаточно для описания оптических процессов и полная информация о квантово-статических свойствах сжатого света требует учета вклада от высших корреляционных функций -поля. Это приводит к выводу важности изучения многоквантовых переходов для анализа статистических свойств самого немонохроматического света. Действительно, высшие корреляционные функции пропорционально вероятностям многоквантовых процессов. Поэтому изучая многоквантовые переходы можно таким образом построить корреляционные функции, которые характеризуют когерентность электромагнитного поля.

Отметим также, что многоквантовый процесс из-за нелинейности может и сам быть источником сжатого света. Однако изучение данного явления выходит за рамки дипломной работы.

1.2. Общие понятия сжатого света

Одним из значительных событий в оптике за последние годы было экспериментальное наблюдение сжатых состояний света [3, 4]. Хотя эти состояния теоретически были предсказаны уже давно, всю важность этого события можно понять, если вспомнить широко распространенную среди оптиков точку зрения, что учет квантового характера света дает лишь малые, шумовые по­правки к тем явлениям, которые описываются неквантовыми уравнениями Максвелла. По существу, эта точка зрения является краеугольным камнем так называемой полуклассической теории, в которой вещество рассматрива­ется на основе квантовых законов, а поле не квантовано, и которой столь многими успехами обязана лазерная и вообще нелинейная оптика. Теперь же после наблюдения сжатых состояний выясняется, что учет квантовой при­роды света приводит к качественно новым явлениям, подобным сжатым состояниям.

В дипломной работе мы не можем осветить все проблемы связанные с сжатым светом (см. обзоры [5, 6]). Основное внимание уделим изложению физической картины сжатого света, его теоретическому описанию и, кратко, возможным применениям. Уделяя основное внимание этим вопросам, нам хо­телось, чтобы читатель почувствовал, с одной стороны, простоту этого явле­ния, а с другой – его довольно общий смысл. Действительно, все изложенное ниже касается состояний в основном квантово-механического гармонического осциллятора и, естественно, справедливо по отношению к любому осцилля­тору, квантование которого производится по бозевской схеме. Следовательно, сжатые состояния кроме оптике могут реализовываться в таких отдаленных друг от друга областях как элементарные частицы (p -мезоны), акустика (фононы) и даже механика (механические колебания). Можно таким образом ожидать наблюдений не только сжатого света, но и сжатого звука (хотя на этом пути могут быть трудности). В принципе возможны даже сжатые состояния при колебаниях таких знакомых и даже обыденных объектов, как маятник или струна. Поэтому мы стремились выделить физи­ческую суть явления сжатых состояний, освободив изложение от излишних технических и математических подробностей.

Наиболее простое объяснение понятия сжатого света приведем в рамках полуклассической квантовой теории. Как известно, существует соотношение неопределенности для импульса и координаты квантовой частицы

Если выполняется равенство, то такое минимизированное квантовое состояние называется когерентным. .

Представим, что мы каким-то образом будем портить данное когерентное состояние путем уменьшения или . Тогда мы получим сжатые состояния. Проиллюстрируем это на рисунке.

Обычно сжатые состояния рассматриваются не в пространстве p x, а в пространстве амплитуда и фаза (амплитудно-сжатое и фазово-сжатое состояния).

Вводится понятие коэффициента сжатия, который качественно отражает "сжатие" продемонстрированное на рисунке.

В оптическом диапазоне при энергии порядка 1 джоуля, запасенной в резо­наторе, коэффициенты сжатия могут достигать значений порядка 1010. Это драматически не совпадает с тем, что достигнуто в экспериментах; в настоящее время реализованы коэффициенты сжатия от нескольких процентов более единицы до нескольких единиц. Пока неясно, в чем причина подобного рас­хождения.

Отметим, что максимальное значение коэффициента сжатия достигается, как отмечено выше, при , т.е. в случае, когда колебания поля отсут­ствуют, . Такие состояния обычно называют сжатым вакуумом. Сле­дует иметь в виду, что сжатый вакуум имеет мало общего с вакуумным (на­инизшим) состоянием; сжатый вакуум может быть высоковозбужденным, высокоэнергичным состоянием.

И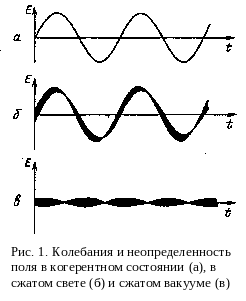зложенные данные приводят к наглядной картине (рис. 1). На рис.1, а изображены колебания при когерентном состоянии поля; не изменяющаяся со временем дисперсия передана толщиной линии. Как обычно при макроскопической энер­гии, дисперсия невелика по сравне­нию с амплитудой. На рис. 1,б изо­бражены колебания при сжатом со­стоянии поля. Здесь уже толщина линии сравнима с амплитудой коле­баний и изменяется со временем. Точка с наименьшей дисперсией мо­жет иметь любую фазу относитель­но колебаний поля. На рис. 1,в изо­бражены "колебания" в состоянии сжатого вакуума. Слово колебания взято в кавычки, так как теперь ко­лебаний с основной частотой  фак­тически нет. Есть только изменения дисперсии с удвоенной частотой.

1.3. Применение сжатого света в информационных системах и системах связи

Применению сжатого света в системах связи посвящено много (пока теоретических) работ. Следует отметить, что сжатый свет не расширяет значительно емкость ин­формационных каналов, максимум – в два раза. Это объясняется тем, что в обычных информационных каналах – без разделения сигнала в приемнике на квадратурные компоненты – детектор регистрирует лишь амплитудные изменения. В системах же с фазовым детектированием фазовый канал также является носителем информации.

О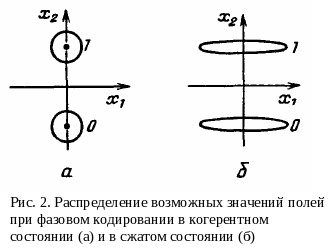днако емкость информационного канала не единственная важная ха­рактеристика системы связи. Очень важной является вероятность появления ошибок, особенно в линиях связи компьютеров. Выигрыш применения сжатого света при этом можно продемонстрировать на примере линии, в которой дво­ичные сигналы 0 и 1 кодируются сигналами, сдвинутыми по фазе на π (рис. 2). При когерентном состоянии (рис. 2, а) сигналы описываются относи­тельно широкими распределениями, из-за перекрытия которых могут возникать квантовые ошибки. При сжатом свете (рис. 2, б) той же интенсивности перекрытие распределений существенно меньше. Расчет показывает, что ве­роятности ошибок при когерентном и сжатом свете соответственно равны

,

где – среднее число фотонов в сигнале, т.е. в сжатом свете вероятность ошибок много меньше.