Дипломная работа: Многоквантовые переходы под действием электромагнитного поля

2.2. Случай немонохроматического поля для многомодового источника

Рассмотрим вероятность перехода под действием излучения многомодового лазера. Применим метод усреднения вероятности перехода в единицу времени под действием монохроматического поля по распределению мод источника. Этот метод справедлив, если , где – ширина верхнего уровня, – спектральная ширина излучения моды. Действительно, ели постоянная времени случайного процесса , можно вычислить вероятность перехода при заданной реализации случайного процесса , затем результат усреднить по всем возможным реализациям с функцией распределения :

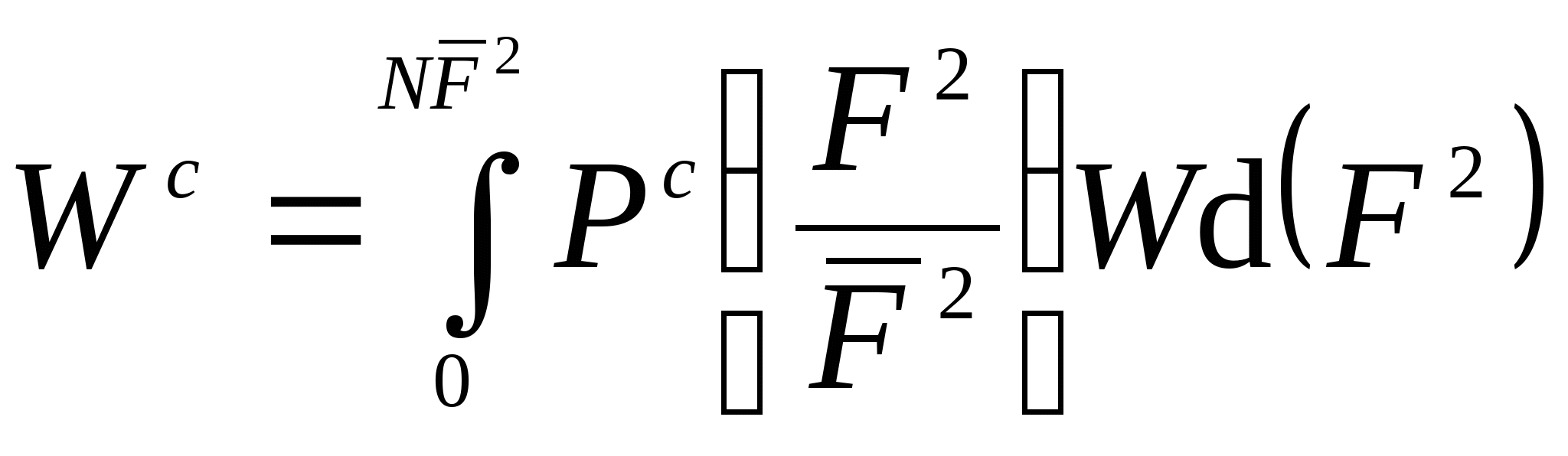
В случае конечного числа мод N функция распределения имеет вид:

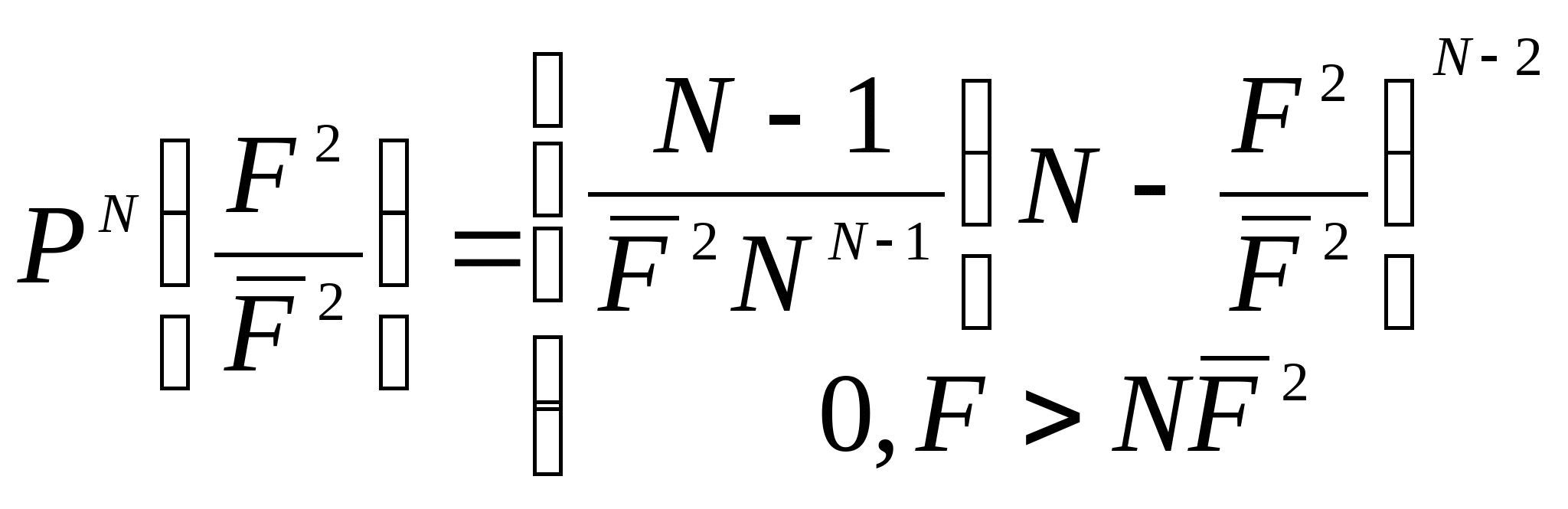
Если , то в качестве функции распределения можно использовать гауссовскую функцию:

Последнее основано на близости статистических свойств многомодового источника к Пуассоновской статистике (относительно энергии ). Хорошо известно, что при малых полях, когда для расчета вероятности перехода достаточно члена для n – квантового процесса, вероятность перехода от многомодового источника в больше, чем вероятность такого же монохроматического источника. Однако, в многомодовом поле уменьшается область применимости теории возмущений, что объясняется существованием влияния выбросов на вероятность перехода.

Для частного случая модели ОДС можно получить аналитическое выражение для вероятности в многомодовом поле. Этот случай рассмотрен в работах Коварского [9], где недиагональное взаимодействие учитывается по теории возмущений, а диагональное – точно, что соответствует малой величине

.

Вероятность перехода в единицу времени в этом случае имеет вид:

, (2.2.1)

– модифицированная функция Бесселя.

Непосредственно виден критерий, при котором выполняется закон (и теория возмущений):

Введем функцию

, (2.2.2)

где

которая получается при подстановке в (2.2.2) формулы (2.2.1)

Для случая произвольных рассмотрим квазиклассическую теорию. Произведем усреднение с функцией распределения. Усреднение с гауссовской весовой функцией в общем случае можно выполнить только численным методом на ЭВМ. Однако при достаточно малых полях в случае ДС его можно найти приближенным интегрированием, воспользовавшись формулой (2.6). При усреднении по гауссовской амплитуде необходимо вычислить интеграл:

,

который в приближении можно оценить методом перевала. Оценка дает:

,

где

,

.

Из приведенной формулы несложно найти критерий применимости теории возмущений для расчета вероятности перехода в единицу времени в случае многомодового источника. Он имеет вид:

.

В случае многомодового источника, критерий применимости теории возмущений не зависит от энергетического расстояния между уровнями. Он более жесткий, чем аналогичный критерий для немонохроматического поля.