Дипломная работа: Моделирование сети кластеризации данных в MATLAB NEURAL NETWORK TOOL

.(2.4)

Таким образом, будет активирован только тот нейрон, вектор весов которого w наиболее близок к входному вектору х. А так как перед началом обучения неизвестно, какой именно нейрон будет активироваться при предъявлении сети конкретного входного вектора, сеть обучается без учителя, т. е. самообучается. Вводя потенциальную функцию — функцию расстояния («соседства») между i-м и j-м нейронами с местоположениями и соответственно, монотонно убывающую с увеличением расстояния между этими нейронами, Кохонен предложил следующий алгоритм коррекции весов:

,(2.5)

где - изменяющийся во времени коэффициент усиления (обычно выбирают на первой итерации, постепенно уменьшая в процессе обучения до нуля); - монотонно убывающая функция.

, (2.6)

Где и - векторы, определяющие положение нейронов i и j в решетке. При принятой метрике функция с ростом времени стремится к нулю. На практике вместо параметра времени используют параметр расстояния , задающий величину области «соседства» и уменьшающийся с течением времени до нуля. Выбор функции также влияет на величины весов всех нейронов в слое. Очевидно, что для нейрона-победителя :

.(2.7)

На рисунке 2.2 показан пример изменения двумерных весов карты , образующей цепь. При появлении входного образа наиболее сильно изменяется весовой вектор нейрона-победителя 5, менее сильно — веса расположенных рядом с ним нейронов 3, 4, 6, 7. А так как нейроны 1, 2, 8, 9 лежат вне области «соседства», их весовые коэффициенты не изменяются.

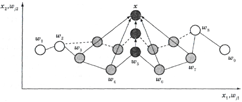
Рисунок– 2.2 Изменение весов карты Кохонена

Таким образом, алгоритм обучения сети Кохонена может быть описан так:

1. Инициализация

Весовым коэффициентам всех нейронов присваиваются малые случайные значения и осуществляется их нормализация. Выбирается соответствующая потенциальная функция и назначается начальное значение коэффициента усиления .

2. Выбор обучающего сигнала

Из всего множества векторов обучающих входных сигналов в соответствии с функцией распределения выбирается один вектор , который представляет «сенсорный сигнал», предъявляемый сети.

3. Анализ отклика (выбор нейрона)

По формуле (2.1) определяется активированный нейрон.

4. Процесс обучения

В соответствии с алгоритмом (2.5) изменяются весовые коэффициенты активированного и соседних с ним нейронов до тех пор, пока не будет получено требуемое значение критерия качества обучения или не будет предъявлено заданное число обучающих входных векторов. Окончательное значение весовых коэффициентов совпадает с нормализованными векторами входов.

Поскольку сеть Кохонена осуществляет проецирование N-мерного пространства образов на М-мерную сеть, анализ сходимости алгоритма обучения представляет собой довольно сложную задачу.

Если бы с каждым нейроном слоя ассоциировался один входной вектор, то вес любого нейрона слоя Кохонена мог бы быть обучен с помощью одного вычисления, так как вес нейрона-победителя корректировался бы с (в соответствии с (2.5) для одномерного случая вес сразу бы попадал в центр отрезка [а, b]). Однако обычно обучающее множество включает множество сходных между собой входных векторов, и сеть Кохонена должна быть обучена активировать один и тот же нейрон для каждого из них. Это достигается усреднением входных векторов путем уменьшения величины, а не при предъявлении каждого последующего входного сигнала. Таким образом, веса, ассоциированные с нейроном, усреднятся и примут значение вблизи «центра» входных сигналов, для которых данный нейрон является «победителем».

2.3 Выбор функции «соседства»

На рисунке 2.3 показан слой нейронов с нейроном-победителем, отмеченным черным кружком. Поскольку веса всех затемненных нейронов изменяются по-разному, в зависимости от их удаленности от нейрона-победителя, наиболее простым является выбор в качестве некоторой величины, равной единице при , меньшей единицы для затемненных нейронов, т. е. нейронов, лежащих в непосредственной близости от активированного нейрона, и нулю для остальных, отмеченных светлыми кружками.

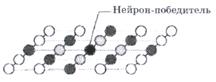
Рисунок 2.3 – Слой нейронов Кохонена

На практике же в качестве выбирают функции, использующие евклидову метрику:

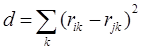, (2.8)

где , — координаты i-гo и j-го нейронов.

К числу наиболее широко используемых потенциальных функций относятся: