Дипломная работа: Обобщение классических средних величин

Действительно, пусть М симметрична. Тогда для некоторого набора различных чисел и произвольной их перестановки или , и поэтому . Обозначив , имеем , где – набор, полученный произвольной перестановкой различных (в силу строгой монотонности функции ) чисел . Покажем, что последнее равенство возможно, только если . Рассуждаем по индукции.

Для n =2 получаем равенство _______________________________________________________________________________________________________________________________ или , откуда .

Предполагая теперь, что наше утверждение верно для какого-нибудь натурального , покажем, что оно будет верным и для , то есть из равенства будет следовать .

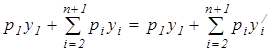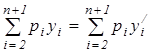В наборе фиксируем , а остальные чисел произвольно переставляем, тогда или , и поэтому по предположению . Аналогично, зафиксировав , получаем . В результате . Индукционный переход обоснован, и мы можем заключить, что наше утверждение верно для любых n .

А так как , то .

4. Свойство однородности.

Также в общем случае, очевидно, не выполняется. Позже мы покажем, что однородными квази-средними будут только средние степенные.

Итак, по слабому определению квази-средние уже являются средними, но сильному определению они удовлетворяют только наполовину. Поэтому мы и назвали такие величины квази (“почти”)-средними.

Глава 2. Квази-средние и функциональные уравнения

Выше мы определили квази-средние напрямую, конструктивно, но оказывается, что можно дать и аксиоматическое определение, то есть предписать им характеристические свойства. С этой целью отдельно рассмотрим несколько функциональных уравнений, которые также будут использованы нами и для выделения основных классов квази-средних. Напомним, что с помощью свойства симметричности один класс мы уже указали – это величины вида .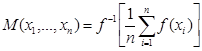

1. Решение некоторых функциональных уравнений

Теорема 1. Единственными непрерывными хотя бы в одной точке решениями следующих уравнений являются соответственно функции:

1. ;

2. ;

3. ;

4. ;

5. ;

6. и , x ≠0;

7. , x >0

Доказательство. 1. Найдём все непрерывные хотя бы в одной точке решения уравнения , которое будет основным, так как мы далее сведём к нему все остальные уравнения.

Зафиксируем точку х₀ из области определения – ту самую, в которой решение непрерывно, и проверим верность равенства для любого r R .

, что возможно только при ;

для любого r N ;

для r =0;

, но тогда и для любого r N , то есть равенство верно для всех целых r .

Далее пусть r Q или r = z / n , где p Z и q N . и поэтому , то есть равенство верно для всех рациональных r .

На последнем шаге используем непрерывность решения в точке х₀ и тот факт, что любое действительное число представляется как предел некоторой рациональной последовательности.

Если , то и , а так как , заключаем, что для любого r R .

Теперь , p R (если обозначить не зависящий от х множитель за p ).