Дипломная работа: Обобщение классических средних величин

Теорема 2. Квази-средние – это такие функции от n переменных, для которых выполнены условия:

1) непрерывность хотя бы в одной точке;

2) ;

3) .

Доказательство. Очевидно, что квази-средние, ранее определённые как удовлетворяют перечисленным свойствам. Важно показать обратное – других величин с данными свойствами не существует. Для этого выведем вид функций , исходя из указанных условий.

Распишем уравнение , используя определение операции :

=

=,

=

=

Далее, если определить и обозначить , , то последнее выражение перепишется так , где функция H непрерывна хотя бы в одной точке. Тогда единственной такой функцией будет , p_i R . Возвращаясь к прежним переменным и функциям, найдём , p_i R .

Осталось показать, что и . Используем свойство усреднения найденного решения: .

Возьмём , но тогда или , и поэтому . А если предположить, что какое-то , то для и , имеем

==

=, что противоречит условию.

Аналогично можно определить квази-средние вида .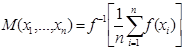

Теорема 3. Квази-средние вида 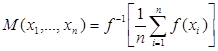– это такие функции от n переменных, для которых выполнены условия:

1) непрерывность хотя бы в одной точке;

2) ;

3) рефлексивность, то есть ;

4) симметричность.

Действительно, свойства 1 и 2 выделяют функции , p_i R , далее свойство 3 обеспечивает , а из свойства 4 вытекает.

Теперь мы можем аксиоматически задавать частные случаи квази-средних, указывая для них свои операции в функциональном уравнении . Например:

для среднего арифметического 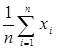задающая его функция , и поэтому ;

для среднего геометрического , ;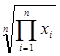

для среднего гармонического , ;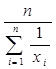

для среднего квадратичного , .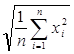

3. Тождественные квази-средние

Квази-среднее 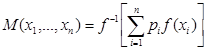определено, если задана функция . Возникает естественный вопрос, справедливо ли обратное предложение: если для любых или и –тождественны, то следует ли отсюда, что задающие их функции и также тождественны. Ответ на этот вопрос даёт следующая