Дипломная работа: Обобщение классических средних величин

Доказательство. Если указанное условие выполняется, то

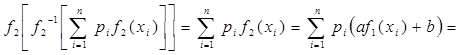
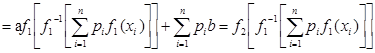, и поэтому

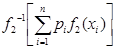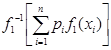= или = для любых , то есть условие достаточно.

Обратно, пусть =, 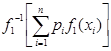= 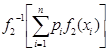или 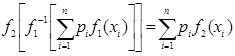. Обозначая и , перепишем =.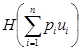

Сведём это равенство к функциональному уравнению. Возьмём точку из области значений функции и представим . Тогда = или =. Полагая , где для каждого i , найдём =, где не зависит от .

Поэтому =, что с обозначениями , , перепишется так: .

Тогда решением этого функционального уравнения будет функция , , где . Так как , то , или, если взять .

Таким образом, чтобы задать одно и то же квази-среднее мы можем взять любую функцию из целого класса функций , где а≠0 и b – произвольные постоянные, и другого способа получить тождественные квази-средние не существует.

4. Однородные квази-средние

Ранее мы говорили, что квази-средние в общем случае неоднородны, то есть соотношение для любых не выполняется, но их подкласс – взвешенные средние степенные обладают однородностью. Теперь покажем, что других квази-средних с данным свойством не существует [2].

Теорема 5. Взвешенные средние степенные – единственные однородные квази-средние.

Доказательство. Предположим, что равенство имеет место, и выведем из него вид задающей квази-среднее функции . Перепишем или =. Получили тождественные квази-средние, заданные функциями и . В силу теоремы 4 имеем (*), где и – функции от λ, ≠ 0. Также мы можем положить .

Тогда . Подставляя теперь в (*) и заменяя λ на y , найдём, что (**). Аналогично .

Последние два равенства дают для x ,