Дипломная работа: Особенности формирования математических понятий в 5 6 классах
Задача учителя – обеспечить полноценное усвоение понятий. Однако в школьной практике данная задача решается не так успешно, как того требуют цели общеобразовательной школы.
«Главный недостаток школьного усвоения понятий – формализм», —считает психолог Н.Ф.Талызина. Суть формализма состоит в том, что учащиеся, правильно воспроизводя определение понятия, то есть, осознавая его содержание, не умеют пользоваться им при решении задач на применение этого понятия. Следовательно, формирование понятий — это важная, актуальная проблема.
Объект исследования: процесс формирования математических понятий в 5-6 классах.
Цель работы: разработать методические рекомендации для изучения математических понятий в 5-6 классах.
Задачи работы:
1. Изучить математическую, методическую, педагогическую литературу по данной теме.
2. Выявить основные способы определения понятий в учебниках 5-6 классов.
3. Определить особенности формирования математических понятий в 5-6 классах.
4. Разработать методические рекомендации формирования некоторых понятий.
Гипотеза исследования : Если в процессе формирования математических понятий в 5-6 классах учесть следующие особенности:
· понятия в большинстве своём определяются с помощью конструирования, и часто формирование правильного представления о понятии у учащихся достигается с помощью поясняющих описаний;
· вводятся понятия конкретно-индуктивным путём;
· на протяжении всего процесса формирования понятия большое внимание уделяется наглядности, то этот процесс будет более эффективным.
Методы исследования:
· изучение методической и психологической литературы по теме;
· сравнение различных учебников по математике;
· опытное преподавание.
Глава 1
Основы методики изучения математических понятий
1.1 Математические понятия, их содержание и объём, классификация понятий
Понятие – форма мышления о целостной совокупности существенных и несущественных свойств объекта. [14]
Математические понятия имеют свои особенности: они часто возникают из потребности науки и не имеют аналогов в реальном мире; они обладают большой степенью абстракции. В силу этого желательно показать учащимся возникновение изучаемого понятия (либо из потребности практики, либо из потребности науки).
Каждое понятие характеризуется объёмом и содержанием. Содержание – множество существенных признаков понятия. Объём – множество объектов, к которым применимо данное понятие. Рассмотрим связь между объёмом и содержанием понятия. Если содержание соответствует действительности и не включает противоречивых признаков, то объём – это не пустое множество, что важно показать учащимся при введении понятия. Содержание вполне определяет объём и наоборот. Значит, изменение одного влечёт изменение другого: если содержание увеличивается, то объём уменьшается. [14]
Содержание понятия отождествляется с его определением, а объём раскрывается через классификацию. Классификация – деление множества на подмножества, которые удовлетворяют следующим требованиям:
o должно проводится по одному признаку;
o классы должны быть не пересекающимися;
o объединение всех классов должно давать всё множество;
o классификация должна быть непрерывной (классами должны быть ближайшие видовые понятия по отношению к понятию, которое подлежит классификации). [14]
Выделяют следующие виды классификации:
1. По видоизмененному признаку. Объекты, подлежащие классификации, могут обладать несколькими признаками, поэтому можно классифицировать по-разному.
Пример. Понятие «треугольник».
| Три стороны равны | Две стороны равны | Нет равных сторон | |
| Остроугольный |  | 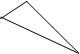 | |
| Прямоугольный | —— | ||
| Тупоугольный | —— |
2. Дихотомический. Деление объёма понятия на два видовых понятия, одно из которых обладает данным признаком, а другое нет.