Дипломная работа: Особенности формирования понятия площади у младших школьников
1) Анализ;
2) Наблюдение;
3) Обобщение;
4) Систематизация.
Этапы исследовательской работы:
1) определение области, проблемы, темы, цели, задачи, объекта и предмета исследования, выдвижение, гипотезы (сентябрь - октябрь 2006 г.);
2) изучение и анализ литературы по теме исследования и оформление теоретической части (ноябрь - январь 2006-07 гг.);
3) определение базы исследовательской работы, проведение опытно-экспериментальной работы (февраль - март 2007 г.);
4) анализ, обобщение результатов исследования, составление рекомендации и оформление дипломной работы (начало апреля 2007 г.);
5) составление списка литературы, оформление титульного листа (конец апреля 2007 г.).
Методологической основой исследования является положение отечественной педагогики, сформулированной в научных трудах педагогов и психологов Истоминой Н.Б., Петерсона Л.Г., Занкова Л.В. и другие.
Научная новизна исследования заключается в выявлении, и поиски новых подходов и методов изучения геометрических величин по альтернативным программам.
Теоретическая значимость заключается в изучении, анализе литературы, выявление эффективных методов, приемов и систематизации формирования понятия площади и ее измерения у младших школьников.
Практическая значимость заключается в том, что материалами исследования могут воспользоваться студенты, учителя начальных классов, методисты, работающие в отделах образования.
Работа состоит из введения, двух глав, выводов, заключения, библиографического списка.
ГЛАВА I . ПОНЯТИЕ ПЛОЩАДИ И ЕЕ ИЗМЕРЕНИЕ
1.1 История развития понятия площади и ее измерения
Зарождение геометрических знаний, связанных с измерением площадей, теряется в глубине тысячелетий.
Еще 4 – 5 тыс. лет назад вавилоняне вычисляли площади земельных участков, имеющих форму прямоугольника и трапеции, в квадратных единицах. Единицей измерения площади издревле использовали квадрат, так как именно квадрат обладает замечательными свойствами: равные стороны, равные и прямые углы; квадрат имеет ось и центр симметрии и совершенство формы. Квадраты легко строить, и ими можно покрыть без просветов фигуры любой формы.
Около 4 000 лет назад египтяне определяли площадь прямоугольника, параллелограмма, треугольника и трапеции теми же приемами, как и мы. То есть, чтобы определить площадь прямоугольника, умножали длину на ширину; чтобы найти площадь треугольника, основание треугольника делили пополам и умножали на высоту. А для нахождения площади трапеции сумму параллельных сторон делили пополам и умножали на высоту. Площадь многоугольника находили разбиением его на прямоугольники, треугольники и трапеции.
Египтяне использовали и иные, которые позволяли быстрее измерять площадь земельного участка путем только обхода его по границам, но результат измерения получался с некоторой погрешностью. Так, площадь равнобедренного треугольника вычисляли по формуле
S=ab 2,
где а – боковая сторона, b – основание треугольника. Совершаемая при этом ошибка тем меньше, чем ближе к 90о угол α между сторонами а и b.
Так как из современной формулы
S=ab 2 sin α D
нам известно, что при α=90о sin 90о =1, S=ab 2. Египтяне также пользовались для вычисления площади четырехугольника ABCD формулой
S=а+b 2 . c+d 2.
При вычислении площади четырехугольников по этой формуле допускалась ошибка. Она минимальна, когда углы четырехугольника близки к прямым. А в случае прямоугольника результат получается точный, так как из формулы
SABCD = AB+CD . AD+BC при AB=CD и AD=BC
получим
SABCD = 2AB. 2AD = AВ АD.
А в случае параллелограмма эта формула дает ощутимую погрешность.
 |  |

![]()
 С С
С С
A D А D
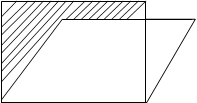
Согласно египетской формуле площади параллелограммов, указанных на рис. 3 и 4, примем равными площадями прямоугольников, построенных на сторонах АD. Заштрихованные площади показывают величину допущенной ошибки в определении площади параллелограмма в двух различных случаях. Если угол СВА параллелограмма по величине далек от прямого, то ошибка может оказаться незначительной.
В математических трудах Евклида, Герона, Брахмагупты и других известно, что по вопросам измерения площадей греки и индусы пошли далеко вперед по сравнению с египтянами и вавилонянами. В своих «Началах» Евклид не применял слово «площадь», так как он под словом «фигура» понимает часть плоскости, ограниченную той или иной замкнутой линией, и под понятием фигуры подразумевал и ее площадь. Евклид результат измерения площади не выражает числом, сравнивает площади различных фигур между собой. Евклид также занимается вопросами превращения одних фигур в равновеликие им фигуры, оперируя при этом не числами, а самими площадями.