Дипломная работа: Особенности формирования понятия площади у младших школьников

где - сторона правильного -угольника . Тогда площадь многоугольника равна

но . Следовательно,

Если -произвольный многоугольник, то его площадь находят, разбивая многоугольник на треугольники (или другие фигуры, для которых известны правила вычисления площади). В связи с этим возникает вопрос: если один и тот же многоугольник по-разному разбить на части и найти их площади, то будут ли полученные суммы площадей частей многоугольника одинаковыми? Доказано, что условиями, сформулированными в определении площади, площадь всякого многоугольника определена однозначно.

Кроме равенства и равновеликости фигур в геометрии рассматривают отношение равносоставленности. С ним связаны важные свойства фигур.

Многоугольники и называются равносоставленными, если их можно разбить на соответственно равные части.

Например, равносоставлены параллелограмм и прямоугольник (рис.3), так как параллелограмм состоит из фигур и , а прямоугольник – из фигур и , причем .

Нетрудно убедиться в том, что равносоставленные фигуры равновелики.

Венгерским математиком Ф.Бойяи и немецким любителем математики П.Гервином была доказана теорема: любые два многоугольника равносоставлены. Другими словами, если два многоугольника имеют равные площади, то их всегда можно представить состоящими из попарно равных частей.

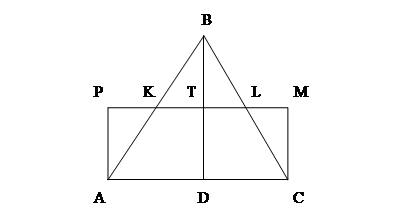
Рис. 4

Теорема Бойяни - Гервина служит теоретической базой для решения задач на перекраивание фигур: одну разрезать на части и сложить из нее другую. Оказывается, что если данные фигуры многоугольные и имеют одинаковые площади, то задача непременно разрешима.

Доказательство теоремы Бойяи-Гервина достаточно сложное. Мы докажем только утверждение о том, что всякий треугольник равносоставлен с некоторым прямоугольником, т.е. всякий треугольник можно перекроить в равновеликий ему прямоугольник.

Пусть дан треугольник (рис.4). Проведем в нем высоту и среднюю линию . Построим прямоугольник, одной стороной которого является , а другая лежит на прямой . Так как пары треугольников и , а также и равны, то треугольник и прямоугольник равносоставлены.

Мы выяснили, что вычисление площади многоугольника сводится по существу к вычислению площадей треугольников, на которые можно разбить этот многоугольник. А как находить площадь произвольной плоской фигуры? И что представляет собой число, выражающее эту площадь?

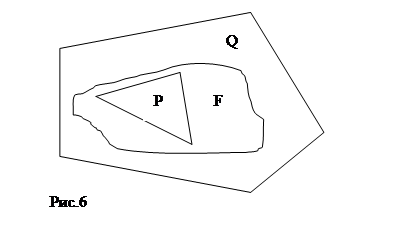
Пусть - произвольная плоская фигура. В геометрии считают, что она имеет площадь , если выполняются следующие условия: существуют многоугольные фигуры, которые содержатся в (назовем их объемлющими); существуют многоугольные фигуры, которые содержаться в (назовем их входящими); площадь этих многоугольных фигур как угодно мало отличаются от . Поясним эти положения. На рисунке 6 показано, что фигура содержит фигуру , т.е. -объемлющая фигура, а фигура содержится в , т.е. - входящая фигура. На теоретико-множественном языке это означает, что и, следовательно, можно записать, что

Если разность площадей объемлющей и входящей фигур может стать как угодно малой, то как установлено в математике, существует единственное число , удовлетворяющее неравенству для любых многоугольных фигур и . Данное число и считают площадью фигуры .

Этими теоретическими положениями пользуются, например, когда выводят формулу площади круга. Для этого в круг радиуса вписывают правильный -угольник , а около окружности описывают правильный -угольник . Если обозначить символами и площади этих многоугольников, то будем иметь, что , причем при возрастании числа сторон вписанных и описанных многоугольников площади будут увеличиваться, оставаясь при этом меньше площади круга, а площади будут уменьшаться, но оставаться больше площади круга.

Площадь правильного -угольника равна половине произведения его периметра на радиус вписанной в него окружности. При возрастании числа его сторон периметр стремится к длине окружности , а площадь - к площади круга. Поэтому

Для приближенного измерения площадей плоских фигур можно использовать различные приборы, в частности, палетку.

Палетка- это прозрачная пластина, на которой нанесена сеть квадратов. Сторона квадрата принимается за 1,