Дипломная работа: Особенности формирования понятия площади у младших школьников
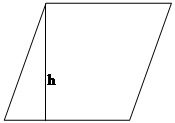
В Древней Руси при вычислении площадей допускали еще одну грубейшую ошибку, полагая, что «фигуры с равными периметрами имеют равные площади». Это предположение неверно ни для одной фигуры, даже если они имеют равные стороны. Например, при равенстве сторон квадрата сторонам ромба площадь квадрата больше площади ромба, так как высота ромба короче его стороны. Докажем это.
Пусть сторона квадрата и сторона ромба равны а.
 В а С
В а С
а а
y
а А Е D
Площадь квадрата
Sкв. =а2
а площадь ромба
Sромба =аh
Из прямоугольного треугольника
АВЕ h=ВЕ=а sin А
Отсюда
Sромба =а. аsinА=а2 sinА
Таким образом, правила, верные для конкретных фигур, неприменимы в более общих случаях.

 2 1 см
2 1 см
3 см 3 см 2 1 см
Возьмем квадрат и равносторонний треугольник с равными периметрами (рис. 12). Для сравнения вычислим площадь равностороннего треугольника с периметром 9 см по формуле
S=1 2 а2 sin α, получим
S=1 2 . 32. sin60о =9 2. 3 2≈9. 1,7 ≈3,8=4(см2 ).
Сторона квадрата с периметром тоже 9 см равна 21 4см, а площадь
S=(2 1 4)2 =(9 4)2 =81 16≈5(cм2 ).
Как видите, площади не равны. Следовательно, нельзя делать вывод о равенстве площадей фигур с равными периметрами.
На ошибках учатся – гласит народная мудрость. Многократно ошибаясь и исправляя собственные ошибки, человек достиг современной высокой культуры вычислений.
1.2 Площадь плоской фигуры и ее измерение
Каждый человек представляет, что такое площадь комнаты, площадь участка земли, площадь поверхности, которую надо покрасить. Он также понимает, что земельные участки одинаковы, то площади их равны; что площадь квартиры складывается из площади комнат и площади других помещений.
Это обыденное представление о площади используется при ее определении в геометрии, где говорят о площади фигуры. Но геометрические фигуры устроены по-разному, и поэтому, когда говорят о площади, выделяют определенный класс фигур. Например, рассматривают площадь многоугольника и др.
Так же, как и при рассмотрении длины отрезка и величины угла, будем использовать понятие «состоять из», определяя его следующим образом:
|
|
|
|

фигура ![]() состоит (составлена) из фигур
состоит (составлена) из фигур ![]() и
и ![]() , если она является их объединением и у них нет общих внутренних точек. В этой же ситуации можно говорить, что фигура
, если она является их объединением и у них нет общих внутренних точек. В этой же ситуации можно говорить, что фигура ![]() разбита на фигуры
разбита на фигуры ![]() и
и ![]() . Например, о фигуре
. Например, о фигуре ![]() , изображенной на рисунке 1,а, можно сказать, что она состоит из фигур
, изображенной на рисунке 1,а, можно сказать, что она состоит из фигур ![]() и
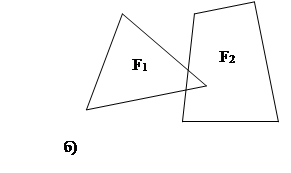
и ![]() , поскольку они не имеют общих внутренних точек. Фигуры
, поскольку они не имеют общих внутренних точек. Фигуры ![]() и
и ![]() на рисунке 1,б имеют общие внутренние точки, поэтому нельзя утверждать, что фигура
на рисунке 1,б имеют общие внутренние точки, поэтому нельзя утверждать, что фигура ![]() состоит из фигур
состоит из фигур ![]() и
и ![]() . Если фигура
. Если фигура ![]() состоит из фигур
состоит из фигур ![]() и
и ![]() , то пишут:
, то пишут:
![]() .
.
Определение. Площадью фигуры называется положительная величина, определённая для каждой фигуры так, что:
1) равные фигуры имеют равные площади;
2) если фигура состоит из двух частей, то её площадь равна сумме площадей этих частей.
Чтобы измерить площадь фигуры, нужно иметь единицу площади. Как правило, такой единицей является площадь квадрата со стороной, равной единичному отрезку. Условимся площадь единичного квадрата обозначать буквой ![]() , а число, которое получается в результате измерения площади фигуры-
, а число, которое получается в результате измерения площади фигуры-![]() . Это число называют численным значением площади фигуры
. Это число называют численным значением площади фигуры ![]() при выбранной единице площади
при выбранной единице площади ![]() . Оно должно удовлетворять условиям:
. Оно должно удовлетворять условиям: