Дипломная работа: Постановка задачи синтеза оптимальных алгоритмов приема сигналов на фоне помех

,

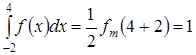откуда .

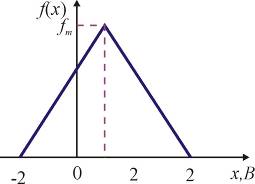
Рис. 14

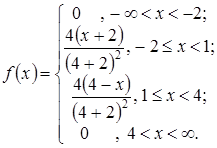
Такое симметричное треугольное распределение называют также законом Симпсона.

В соответствии с определениями математическое ожидание и дисперсия равны

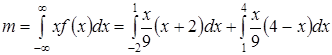= 1 В;

.

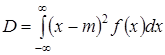Однако удобнее вычислить вначале второй начальный момент

= 7 В2,

тогда = 6 В2.

Смешанные начальные моменты определяются соотношением

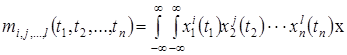
. (5)

Смешанные центральные моменты определяются аналогично, но с заменой x в формуле (5) на центрированное значение .

Ввиду того, что значения x в смешанных моментах определяются в различные моменты времени, появляется возможность оценки статистической взаимозависимости значений процессов, разделенных заданными интервалами. Наиболее важным является простейший из смешанных моментов, отображающий линейную статистическую взаимозависимость и называется корреляционной и ковариационной функцией:

;

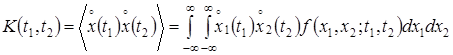. (6)

Как видно из определения, размерность корреляционной функции определяется размерностью квадрата величины x (для напряжения – В2).

Для стационарного СП корреляционная функция зависит только от разности :

.

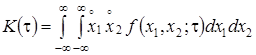Следует заметить, что при t = 0 максимальное значение K(0) = s2.

На рис. 15 приведены примеры реализаций процессов с разными корреляционными функциями.

Кроме функционалов на основе степенных функций (моментов) возможны и другие типы функционалов в качестве статистических характеристик СП. Важнейшим среди них является функционал, основанный на экспоненциальном преобразовании и называемый характеристической функцией

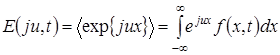. (7)

Нетрудно заметить, что данное выражение представляет преобразование Фурье от плотности вероятности, отличающееся от обычного лишь знаком в показателе экспоненты.

Поэтому можно записать и обратное преобразование, позволяющее по характеристической функции восстановить плотность вероятности:

.
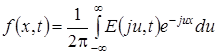