Дипломная работа: Постановка задачи синтеза оптимальных алгоритмов приема сигналов на фоне помех

– свойство ограниченности , для стационарных процессов ;

– свойство неограниченного убывания с ростом аргумента (для эргодических процессов) ;

– свойство положительной определенности интеграла

;

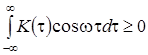– размерность соответствует квадрату размерности случайного процесса.

Это свойство следует из определения спектральной плотности мощности (для случайных напряжений и тока через сопротивление 1 Ом), которое будет приведено ниже.

Для взаимнокорреляционной функции аналогично можно записать:

; ;

; .

Ввиду ограниченности корреляционной функции частот используют нормированные корреляционные функции

; ,

причем ; .

Для более компактного описания свойств случайного процесса вводят понятие интервала корреляции, определяющего интервал времени, на котором существует связь между значениями процесса.

Основные определения интервала корреляции:

– интегральный (для положительно определенных корреляционных функций) . Геометрически он характеризует ширину основания прямоугольника, равновеликого по площади функции k(t) при t > 0 (рис. 17а);

– абсолютный интервал корреляции (в отличие от предыдущего может использоваться для знакопеременных функций ) (рис. 17б);

– квадратичный интервал корреляции ;

– максимальный интервал корреляции (на уровне a) (рис. 18)

.

Рис. 17

Рис. 18

Обычно уровень a выбирается исходя из рассматриваемой задачи и имеет значения 1/e; 0,1; 9,05; 0,01 и т.д.

Последнее определение не является более произвольным, чем предыдущие, так как выбор конкретного вида функционала протяженности произволен и определяется удобством математического решения конкретной задачи. Практически этот интервал корреляции используется в радиоизмерениях для определения интервала, вне которого случайные величины в сечениях случайного процесса можно считать некоррелированными. Достоверность такого предположения определяется выбором уровня a.

Большое значение в статистической радиотехнике имеют спектральные характеристики СП. При этом используются различные интегральные преобразования процесса вида

.

При исследовании линейных систем с постоянными параметрами особое значение имеет ядро преобразования вида , так как отклик линейных систем на гармоническое воздействие также является гармоническим.

Преобразование Фурье от k-й реализации СП дает также случайную функцию частоты, зависящую от номера реализации: