Квантование по времени делает всю систему управления дискретной (рисунок 1.14), а по уровню нелинейной. Разрядная сетка современных ЭВМ такова, что влиянием квантования по уровню можно пренебречь. Это делает всю систему линейной и позволяет использовать для ее расчета математический аппарат исследования импульсных систем.

Цифровой сигнал, отражающий преобразованный непрерывный сигнал в дискретный, представляет собой двоичное число - совокупность логических нулей и единиц. При исследовании цифровых систем автоматического управления этот реальный сигнал заменяют его математической абстракцией - решетчатой функцией.

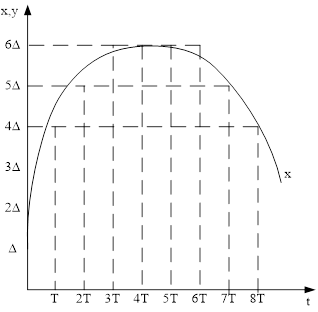
Рисунок 1.14 - График квантования сигнала по времени

Понятие решетчатой функции лежит в основе математического описания дискретных систем и позволяет осуществлять переход к дискретному аналогу дифференциальных уравнений - разностным уравнением (уравнения в конечных разностях). Эти уравнения, определяющие связь между значениями решетчатой функции с помощью конечных разностей, являются аналогами производных в дифференциальных уравнениях [8].

Первая прямая разность:

(1.2)

получается путем вычитания из последующего значения решетчатой функции (будущего) текущего значения.

Первая обратная разность:

(1.3)

получается путем вычитания из текущего значения предыдущего.

Первая разность является аналогом первой производной непрерывной функции.

Для решения разностных уравнений широко применяется Z-преобразование, оно вытекает из дискретного преобразования Лапласа решетчатых функций.

Преобразование Лапласа

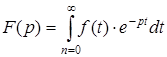. (1.4)

Дискретное преобразование Лапласа для решетчатых функций

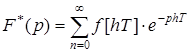. (1.5)

Z-преобразование решетчатой функции

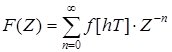, (1.6)

где ,

n = 0, 1, 2, …. .

Таким образом, решетчатая исходная функция заменяется ее изображением (Z-преобразованием). Переход от оригинала к изображению позволяет заменить решение разностных уравнений - решением алгебраических.

2. Выбор структуры и расчет параметров регулятора

В литературе [8] приводятся примеры аппроксимации линейных регуляторов заменой операции дифференцирования на первую разность. При этом имеется возможность использовать накопленный опыт работы с аналоговыми регуляторами и применять известные правила настройки регуляторов.

Для определения структуры цифрового КУ аппроксимируем передаточную функцию аналогового регулятора, настроенного на оптимальную работу. Исследуем влияние изменения коэффициентов регулятора, на качество управления и характер переходного процесса, и определим значения коэффициентов, при которых обеспечиваются наилучшие динамические характеристики электропривода.

Так же ставится задача исследования устойчивости электропривода с разработанным регулятором.

2.1 Расчет линейного регулятора

Для расчета линейного регулятора, используем модель электропривода, приведенную на рисунке 2.1 Так как в электроприводе с фазовой синхронизацией главной целью является отработка фазового рассогласования по углу поворота вала, то в качестве выходной координаты удобно принять ошибку по углу Δα. В качестве оптимального режима, примем критический переходный процесс [1].

Преобразуем структурную схему (рисунок 1.12) к виду, показанному на рисунке 2.1.

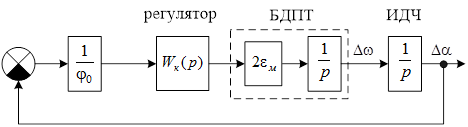
Рисунок 2.1 - Преобразованная структурная схема электропривода с фазовой синхронизацией