Дипломная работа: Расчет квантово-химических параметров ФАВ и определение зависимости "структура-активность" на примере сульфаниламидов
Основа для такого предсказания известна достаточно давно, и она связана с утверждением: "Биологическая активность вещества является функцией его химической структуры ". Надо "всего лишь" выявить вид этой функции и в дальнейшем "подставить в уравнение" структурную формулу исследуемого вещества, получив в результате прогностическую оценку его биологической активности. В сущности, именно так и поступают в медицинской химии: анализируя химическое строение соединений с известной биологической активностью, выделяют элементы, "ответственные" за проявление/отсутствие того или иного эффектов, и далее "конструируют" молекулы более активных и менее токсичных аналогов. [6]
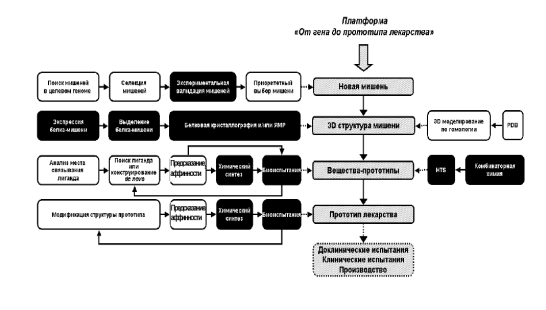
Рисунок 1.1 Общая структура платформы от гена до прототипа лекарства. Экспериментальные блоки показаны черным цветом, компьютерные – белым.
Это положение послужило основанием для выделения у химических соединений определенных факторов (дескрипторов) и установления связи, качественной (SAR) или количественной (QSAR), между ними и биологической активностью соединения. В качестве таких дескрипторов используются различные характеристики молекулы:
1. топологические – фрагменты структуры (подструктурные дескрипторы), индексы атомов и связей, каппа - индексы, описывающие форму молекулы, индексы молекулярных связей (MCI);
2. квантовые параметры – энергии HOMO (высшей занятой обитали) и LUMO (низшей незанятой обитали), заряды на различных атомах, электронные плотности, поляризуемости;
3. параметры, относящиеся к целой молекуле – молярная рефракция, коэффициент распределения октанол - вода.
В данной работе будет рассмотрена возможность проведения анализа «структура вещества – проявляемая физиологическая активность» на примере соединений сульфаниламидного ряда. Сульфаниламиды относятся к лекарственным веществам противостафилакоккового направления бактериостатического принципа действия. Так же они проявляют антидиабетические, диуретические и антисептические свойства. Более подробно сульфаниламиды рассмотрены в главе 3.
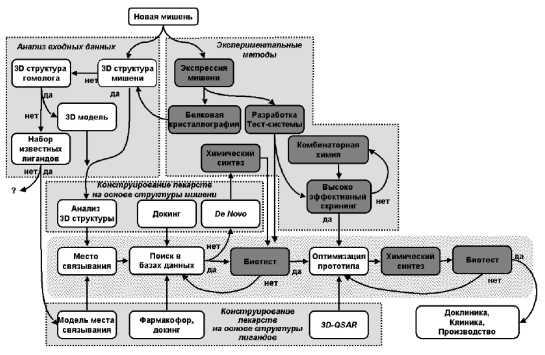
Рисунок 1.2 Общая схема стратегии компьютерного конструирования лекарств.
Квантовая механика и статистическая физика в принципе позволяют дать исчерпывающее объяснение любым экспериментальным данным о реакционной способности органических соединений и предсказать возможные направления реакций, а так же виды проявляемой физиологической активности.
В данной работе будет рассмотрена возможность не только расчета параметров соединения, что позволит химикам – синтетикам еще до получения конкретного соединения предсказать его физико – химические свойства, но и будет предложен метод для расчета физиологической активности соединения. Ни в зарубежной, ни в отечественной литературе эти методы ранее в совокупности не рассматривались, и возможности перехода от одного к другому не исследовались.
Глава 1 МАТЕМАТИЧЕСКИЕ МЕТОДЫ РАСЧЕТА КОНСТАНТ ОРГАНИЧЕСКИХ МОЛЕКУЛ И ВИДОВ ПРОЯВЛЯЕМОЙ ФИЗИОЛОГИЧЕСКОЙ АКТИВНОСТИ
1.1 История развития квантовохимических методов анализа «структура вещества – проявляемая физиологическая активность»
В основе квантовой механики лежит уравнение Шредингера, играющее в ней такую же важную роль, как и уравнения Ньютона в классической механике. Также как и уравнения Ньютона, уравнение Шредингера не выведено ни из какой физической теории, а является постулатом, полученным в результате обобщения опытных фактов.
Для совокупности Nвзаимодействующих частиц с потенциальной энергией U и массами mk в декартовой системе координат оно имеет вид
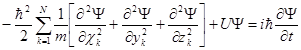
где Ψ(x, y, z, t) – волновая функция совокупности координат системы частиц и времени, U – оператор потенциальной энергии. Суммирование производится по всем частицам.
Стационарные состояния удовлетворяют не зависящему от времени уравнению Шредингера:
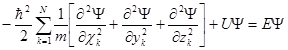
Параметр Е есть собственное значение стационарного уравнения Шредингера. В результате решения стационарного уравнения Шредингера находят собственные (возможные) значения параметра Е и соответствующие ему решения – собственные функции.
Для любого уравнения Шредингера, соответствующего конкретной системе, существует бесконечное множество значений параметра Е. Эти значения могут быть как непрерывными (для свободно движущейся частицы), так и дискретными, если частицы локализованы в малой области пространства. Дискретные значения Е называют уровнями энергии.
Пользуясь операторной символикой, можно записать уравнение Шредингера в сокращенной форме:
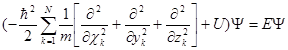
ĤΨ = ЕΨ,
где Ĥ = 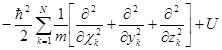 - оператор Гамильтона или гамильтониан системы частиц.
- оператор Гамильтона или гамильтониан системы частиц.
1970 - 1980-е годы были временем очень быстрого развития вычислительных методов квантовой химии. В результате появилась возможность рассчитывать геометрию и оценивать стабильность промежуточных продуктов и переходных состояний, а также вычислять профили поверхности потенциальной энергии вдоль координаты реакции. Экспериментальное получение подобной информации для большинства реакций связано с преодолением значительных трудностей, вызванных многостадийным характером процессов, синхронным протеканием отдельных элементарных стадий и очень малым временем жизни промежуточных продуктов. Развитие вычислительных методов квантовой химии и появление быстродействующих ЭВМ позволили рассчитывать многие характеристики органических соединений, в том числе и нестабильных, а также переходных состояний. Точность этих расчетов получается вполне удовлетворительной по термохимическим стандартам. Поэтому квантовохимические расчеты в настоящее время используются в качестве одного из физико-химических методов исследования для получения данных, необходимых для установления механизмов сложных органических реакций.
Существующие методы математического моделирования "структура- активность" могут быть условно разделены на три группы.
Первая группа основана на использовании принципа линейности свободных энергий и включает в себя такие подходы, как метод Хэнча, метод Кубиньи и "диффузионный подход".
К этой же группе причисляют аддитивно- статистические методы Фри - Уилсона, Фуйита - Бана, Каммарата - Яу и им подобные. Для построения моделей, реализующих принцип линейности свободных энергий, используются методы регрессионного анализа.
Вторая группа объединяет методы, предназначенные для получения первоначальных представлений об изучаемом явлении посредством статистической обработки всей имеющейся информации, а также преобразования ее к виду, удобному для дальнейшего использования. Эта группа методов иногда называется методами "генерации гипотез". Она объединяет такие методы, как факторный анализ во всех его модификациях, методы линейного отображения, иногда к этой группе относят и аддитивно- статистические методы.