Дипломная работа: Расчет квантово-химических параметров ФАВ и определение зависимости "структура-активность" на примере сульфаниламидов

Эта модель основана на предположении о том, что вклад данного заместителя, находящегося в структуре в данном положении, всегда одинаков независимо от того, в каком соединении присутствует рассматриваемый заместитель. Величины вкладов заместителей рассчитываются с помощью множественного линейного регрессионного анализа. Для построения линии регрессии необходима только информация о молекулярной структуре и биологической активности соединений, никакие физико-химические параметры не используются.

При анализе данных методом Фри - Вильсона для каждого соединения составляется линейное уравнение, а параметры рассчитываются методом наименьших квадратов. Здесь применяются те же статистические критерии, что и при анализе методом Ханша. Если рассчитанные статистические критерии являются удовлетворительными и тем самым обоснована применимость аддитивной схемы, то с помощью полученных таким образом параметров линейного соотношения можно восстановить величины биологической активности соединений, составляющих исходную выборку. При этом отдельные сильные отклонения от линейной зависимости могут быть сразу же идентифицированы. И наконец, наиболее важный результат состоит в том, что с помощью рассчитанных значений параметров можно предсказать активность соединений, образованных путем всевозможных сочетаний и перестановок исходных заместителей. Относительные вклады в биологическую активность различных заместителей, расположенных в соединении в различных положениях, могут быть упорядочены

Главный недостаток метода Фри — Вильсона заключается в том, что для описания всех заместителей требуется очень большое число переменных. К тому же иногда приходится иметь дело с вырожденными матрицами. Таким образом, при использовании метода Фри — Вильсона исследователю приходится выбирать одну из двух возможностей: либо испытывать большое количество производных, либо ограничивать количество заместителей и их положений в структуре. Результат выбора, очевидно, определяется спецификой конкретной задачи.

1.1.6 Метод Хюккеля, расширенный метод Хюккеля

Исторически метод, предложенный Эрихом Хюккелем в 1931 г., являлся первым полуэмпирическим квантово - химическим методом. В настоящее время он используется лишь для качественного объяснения свойств главным образом π - сопряженных молекул. Для количественных расчетов используется вариант данного метода, введенный в практику в 1961 г. Р. Хоффманом и получивший название расширенного метода Хюккеля. Он является простейшим, наиболее быстрым и вместе с тем наименее точным полуэмпирическим квантово-химическим методом. Его использование ограничивается в основном анализом структуры молекулярных орбиталей — определением их формы и последовательности.

Электрон - электронное взаимодействие в этом методе в явном виде не учитывается, диагональные элементы матрицы Н аппроксимируются потенциалами ионизации, взятыми с обратным знаком, а для недиагональных членов используется одно из приближений.

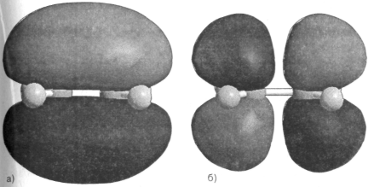
Рисунок 1.7.1. Вид молекулярных орбиталей HOMO (а) и LUMО (б) молекулы этилена, рассчитанных расширенным методом Хюккеля в программе HyperChem 7.0.

Подобный подход хорошо работает при расчете систем с относительно равномерным распределением заряда, например углеводородов, для которых он и был первоначально использован. Однако даже и в таких случаях бывают казусы. Например, в соответствии с предсказанием расчета, бензол должен распадаться на три молекулы ацетилена с выделением значительного количества теплоты. Что касается систем, содержащих гетероатомы, то для них более адекватным является интегративный расширенный метод Хюккеля. В этом методе уже учитывается зависимость гамильтониана от заряда на данном центре, причем зависимость полагается линейной.

1.2 Современные методы анализа «структура вещества – проявляемая физиологическая активность»

1.2.1 Принципы распознавания образов

Одна из основных предпосылок методов конструирования лекарств — предположение о том, что соединения сходной структуры имеют сходные типы биологической активности. Очень трудно дать строгое определение понятия структурного сходства, о чем свидетельствует обилие и разнообразие параметров, используемых при выводе эмпирических соотношений, связывающих структуру соединений с их биологической активностью. До сих пор наиболее распространенным методом чтения координат и методом построения таких соотношений был регрессионный анализ. Целью этого подхода является построение эмпирических соотношений, связывающих различные сочетания физических, химических или структурных параметров с биологической реакцией соединения. Этот метод особенно эффективен при исследовании не слишком длинных гомологических рядов соединений.

Методам распознавания образов посвящено множество монографий [16]. Этот факт, несомненно, является отражением широкой применимости методов распознавания. Применение методов распознавания образов к химическим задачам началось в середине 1960-х годов в связи с масс-спектральными исследованиями. После этого аналогичные работы стали проводиться во многих других областях химии.

Одна из интересных особенностей этих методов заключается в том, что они могут иметь дело с многомерными данными, т. е. данными, в которых для представления каждого объекта используется более трех параметров. К тому же этими методами можно анализировать данные, полученные из разных источников, а также данные, связи между которыми имеют разрывный характер. При соответствующем подходе методы распознавания образов дают возможность установить критерий отбора из исходного множества данных тех параметров, которые существенны для описания исследуемых свойств. Далее с помощью этого набора наиболее значимых признаков могут быть получены указания о направлении дальнейших исследований.

1.2.2 Основные понятия методов распознавания образов

Прежде чем начать обсуждение методов распознавания образов, необходимо объяснить, что подразумевается под классификацией объекта или группы объектов. В процессе классификации формируется правило разделения группы объектов на несколько категорий, а при распознавании это классификационное правило используется для отнесения неизвестного объекта к одной из рассматриваемых категорий. Классификационное правило устанавливается в виде некоторой гипотезы, полученной в результате анализа экспериментальных данных. Проверка правильности этой гипотезы проводится путем ее испытания на объектах, не включенных в группу данных, с помощью которых было получено классификационное правило. В случае удачных испытаний гипотеза считается правильной. Процесс классификации заключается не только в выработке классификационного правила и его дальнейшего применения для распознавания. Ниже на простом примере будут продемонстрированы основные особенности задачи распознавания образов.

В качестве примера построения классификационного правила рассмотрим следующую воображаемую задачу. Предположим, что мы хотим автоматизировать процесс идентификации аномальных клеток при анализе крови в клинической лаборатории. Попробуем составить опытный проект оптической воспринимающей системы, способной отличить лейкимические клетки от здоровых на основе оптической проницаемости (рис. 2.1.1). Будем считать, что если прозрачность клетки превосходит некоторый уровень Хо, то она относится к лейкемическим клеткам.

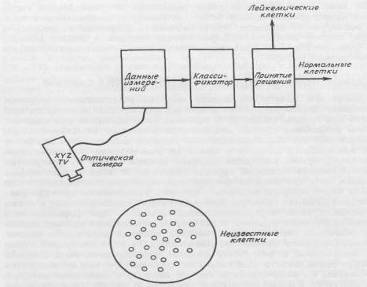
Рисунок 2.1.1 Схема оптической системы распознавания образов

Поскольку надежность такой классификации слишком низка, необходимо искать дополнительные признаки, которые могли бы оказаться полезными при различении разных типов клеток. Предположим, что лейкимические клетки имеют более ярко выраженную клеточную структуру, чем нормальные. В этом случае можно настроить камеру на измерение контрастности образцов и таким образом получить характеристику структурированности для каждой клетки эталонного набора образцов. В результате получим двумерную диаграмму, показанную на рис. 2.1.2

Цель методов отбора признаков — добиться наибольшего эффекта наименьшим числом признаков. Сокращение количества необходимых признаков облегчает процедуру классификации и в некоторых случаях увеличивает надежность результатов.

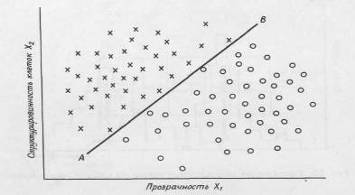
Рисунок 2.1.2 Разделение образов клеток на два класса в пространстве двух признаков — структурированности и прозрачности клеток.

Вся процедура распознавания образов складывается из трех последовательных операций: измерения, предварительной обработки и классификации. В результате применения этих операций последовательно формируются пространство измерений, пространство признаков и классификационное правило. Разделение всей процедуры распознавания образов на три стадии является несколько условным, поскольку приемы, используемые в одной из стадий, часто с успехом могут применяться и на других этапах обработки.

Предварительная обработка

С помощью методов предварительной обработки проводится преобразование исходных данных. К методам предварительной обработки относятся: масштабирование, нормализация, преобразования кластеризации, отбор признаков, многомерный скейлинг и нелинейное отображение.

Масштабирование и нормализация

Для преобразования данных, полученных разными датчиками, к виду, удобному для обработки, необходимо выбрать масштаб и выполнить нормализацию. Эти преобразования особенно важны, когда данные получены из разных источников. В этом случае они могут отличаться на несколько порядков величины, так что большие по величине дескрипторы будут подавлять малые. Этот недостаток может быть устранен путем автоматического выбора масштаба [17].

После преобразования масштаба желательно таким образом преобразовать данные, чтобы измерения, дающие больший вклад в кластеризацию, имели соответственно большие веса. Одним из простейших методов такого преобразования является метод дисперсионного взвешивания.

Хотя процедуры типа масштабирования могут уменьшить эффект разнородности исходных данных, а в методе дисперсионного взвешивания признаки получают веса, соответствующие их вкладу в кластеризацию, обе эти операции изменяют исходные данные одинаково.

Одним из недостатков методов предварительной обработки данных является то, что они учитывают все признаки, в том числе и те, которые могут не иметь отношения к рассматриваемой классификационной задаче. В результате возможно попадание в весьма неблагоприятную ситуацию, особенно в том случае, если несущественные признаки будут увеличивать ошибку процедуры классификации, не говоря уже о сложности и стоимо