Дипломная работа: Рассеяние электронной плотности в металлах и ионных кристаллах по рентгенографическим данным

электронный плотность комптоновский рассеяние

Рис. 1.2. 1Кривые энергии межатомного взаимодействия: I -для сильной (ионной, ковалентной, металлической) связи, II -для слабой (ван-дер-ваальсовой) связи.

Рис. 1.2.2 Распределение электронной плотности на линии связи между атомами в кристаллах: а- ионная связь (NaCl), пунктирная линия - область внешних электронных орбит; б - металлическая связь (А1), пунктирная линия - плотность электронов в межатомном пространстве.

В ионных кристаллах внешние валентные электроны переходят от атомов металлов, которые становятся положительными ионами (катионами), к атомам неметаллов, которые становятся отрицательными ионами (анионами), что приводит к электростатическому притяжению между ними (рис. 1.2.2). Взаимодействие ионов является кулоновским, но при их соприкосновении начинают играть роль силы отталкивания между электронными оболочками; потенциальная энергия их взаимодействия описывается формулой

где r - расстояние между центрами ионов; b и п - параметры, которые могут быть найдены из сжимаемости кристаллов; n =(6-9). В межатомном пространстве в ионных кристаллах электронная плотность r (r )близка к нулю рис. 1.2.2, а.

Потенциальная энергия взаимодействия рассчитывается по формуле:

где m =4, а, α, С - константы, более точно u _ков получают из решения методами квантовой химии уравнения Шрёдингера.

Природа металлической связи та же, что и ковалентной, т. е. обобществление внешних валентных электронов атомов, однако характер локализации этих электронов иной - они приблизительно равномерно заполняют всё межатомное пространство, образуя общий электронный "газ", который и осуществляет коллективное взаимодействие с заряженными положительно атомами металла (рис. 1.2.2, б)

В молекулярных кристаллах атомы внутри молекул объединены прочными ковалентными связями, а атомы соседних молекул взаимодействуют за счёт более слабых ван-дер-ваальсовых сил, имеющих дипольное и дисперсионное происхождение. Расстояние между атомами соседних молекул 0,35-0,4 нм.

В работе о распределении электронной плотности и потенциала в решетке селенида марганца описывается разностный метод расчета электронной плотности.[4] В качестве исследуемого вещества выбран селенид марганца. По измеренным значениям интенсивностей подсчитывались абсолютные значения структурных амплитуд. При этом вводились поправки на дисперсию и температурный фактор.[5]

Измеренные структурные амплитуды ( F ) для селенида марганца представлены на рис. 1.2.3, а, где сплошными линиями нанесены теоретические значения F , рассчитанные по Хартри - Фоку для нейтральных атомов [6]. Как видно из рисунка, экспериментальные значения структурных амплитуд определяющиеся разностью f_Se – f_Mn , при малых значениях лежат выше теоретических.

Подсчитанные по структурным амплитудам функции атомного рассеяния (рис. 1.2.3, б) при малых значениях H, также отличались от теоретических, причем для селена экспериментальные значения лежат выше теоретических, а для марганца ниже теоретических. Таким образом, полученные данные показали, что в решетке селенида марганца

Рис. 1.2.3 Структурные амплитуды (а) и функции атомного рассеяния ионов (б)

ионы марганцаимеют положительный заряд, а ионы селена отрицательный. Для оценки величины заряда ионов был выполнен разностный синтез трехмерного ряда Фурье

(1.2.1)

для направлений [100], [110] и [111], результаты которого показали, что электронная плотность в области иона марганца уменьшается ( отрицательно), а в области иона селена увеличивается. Численный расчет показал, что величина заряда ионов в селениде марганца составляет примерно 1,2 ±0,2 эл. По полученным данным f-функций подсчитывалась электронная плотность в решетке MnSe между ионами марганца и селена с использованием разностного метода синтеза трехмерного ряда Фурье: [7]

(1.2.2)

где F ₁ —структурная амплитуда преимущественно внутренних электронов, функция рассеяния которых аппроксимировалась в виде

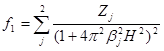(1.2.3)

Коэффициенты Z_j и определялись по данным привязки к f - функции при больших порядках отражения с использованием теоретических значений.

Расчеты электронной плотности показали (рис, 1.2.4), что в направлении [100] между ближайшими ионами Mn-Se минимальное значение плотности электронов составляет примерно 0,15 эл/А³ и в направлении [110] между ионами Мn-Мn оно падает практически до нуля.

Для соединения МnО плотность между ближайшими ионами Мn - О в несколько раз больше, чем в MnSe, и составляет примерно 0,55 эл/А³ , Это обстоятельство указывает на то, что в селениде марганца ковалентная составляющая связи значительно меньше, чём в закиси марганца, и MnSe является близким к чисто ионным кристаллам. [8]

Из измеренных экспериментальных функций атомного рассеяния ионов, входящих в состав соединения селенида марганца, было рассчитано распределение потенциала в решетке данного соединения. Распределение потенциала в решетке выражалось трехмерным рядом Фурье

, (1.2.4)

где структурная амплитуда

.

Как видно из соотношения (1.2.4), распределение потенциала подсчитывалось непосредственно по экспериментальным значениям f - функций, полученным из данных интенсивности рентгеновских дифракционных спектров.

Расчеты показали, что если f - кривая какого-либо иона аппроксимируется выражением вида

,

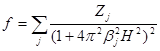то электронная плотность и потенциал этого иона будутописываться выражением

,

,

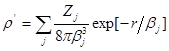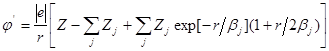где определяет степень ионизации рассматриваемогоиона.

Таким образом, чтобы подсчитать значение потенциала в какой-либо точке решетки, необходимо просуммировать значения потенциалов в данной точке от всех окружающих ионов. Наибольший вклад вносили ионы, расположённые на первой и второй координационных сферах, так как от более удаленных ионов вклады уменьшаются как за счет расстояния, так и за счет взаимной компенсации ионов противоположного знака.

В работе[9] рассматривается распределение валентной электронной плотности в преимущественно ионных кристаллах с различающимися подрешетками Браве. Выяснилось, что в случае кристаллов с различающимися подрешетками Браве анионная подрешетка представляла собой ковалентно связанный каркас, в который помещалась подрешетка металла.

В качестве величины, характеризующей связь подрешеток, использовалась разностная плотность, полученная как результат вычитания из кристаллической электронной плотности плотностей отдельных подрешеток. Разностная плотность исследованных кристаллов оказывалась на порядок меньше кристаллической и подрешеточных, что свидетельствовало о слабой гибридизации подрешеток и преимущественно ионном характере связи между ними.

В работе [10] рассматривается перераспределения электронной плотности в области точечных дефектов в алюминии методом функционала электронной плотности.

Для правильного определения механизмов диффузии говорится о необходимости использования новых, более точных и корректных методов моделирования точечных дефектов и их комплексов в металлах и сплавах.