Дипломная работа: Рассеяние электронной плотности в металлах и ионных кристаллах по рентгенографическим данным

В настоящее время наиболее перспективным и точным методом расчета характеристик точечных дефектов в металлах является метод функционала электронной плотности. Это единственный метод, который позволяет учитывать перераспределение электронной плотности в области точечных дефектов. Также к преимуществам данного метода следует отнести тот факт, что для расчетов он не требует экспериментальных данных и подгоночных констант, а основан исключительно на фундаментальных константах, таких как заряд ядра и электронное строение атома. К недостаткам данного метода следует отнести невозможность расчета систем размером более сотен атомов и необходимость использовать достаточно мощные вычислительные системы.

В основу теории функционала электронной плотности положена теорема Хоэнберга и Кона, согласно которой все свойства основного состояния неоднородного взаимодействующего электронного газа могут быть описаны с помощью введения некоторых функционалов от электронной плотности . Вместо обычного гамильтониана системы вводится функционал следующей структуры:

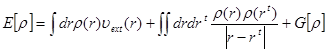
где v_ext ( r ) - внешнее поле, в которое входит поле ядер; функционал G [ p ] является универсальным и не зависит от внешнего поля. [11]

С помощью метода функционала электронной плотности, было проведено моделирование моновакансии в чистом алюминии. Моделирование проводилось для ячейки 4x4x4 (256 атомов).

Для бездефектного алюминия был определен параметр решетки, который равен а_А! = 4,0468 Ǻ, что хорошо согласуется как с другими работами по моделированию , так и с экспериментальными данными.

Для алюминия содержащего моновакансию, была определена ее энергия образования, которая равна 0,66 эВ, что хорошо согласуется с работами, сделанными ранее, а также проведен расчет перераспределения электронной плотности при образовании вакансии (разность функций распределения электронной плотности в бездефектном алюминии и алюминии с вакансией). [12,13]

В работе [14] рассматривается расчет распределения электронной плотности и потенциала в алмазе по рентгенографическим данным. Распределение электронной плотности задается рядом Фурье

, (1.2.5)

где F_hkl - экспериментально измеренные величины структурных амплитуд, H – вектор обратной решетки, абсолютная величина которого дается соотношением

,

R –радиус-вектор точки с координатами (x ,y ,z ), для которой определяется электронная плотность, V – объем элементарной ячейки.

Зная интегральные интенсивности дифракционных максимумов I_hkl , может быть определена следующего соотношения структурная амплитуда F_{hkl :}

,

где I ₀ – интенсивность первичного рентгеновского пучка, падающего на исследуемый образец, А^* - произведение всех коэффициентов, входящих в выражение для интенсивности брегговского рефлекса.

Ряд (1.2.5) оказывается слабо сходящимся и его вычисление для известных значений структурных амплитуд может привести к непредсказуемым погрешностям. С другой стороны, распределение плотности заряда, как во всем кристалле, так и в его элементарной ячейке может быть описано уравнением Пуассона:

(1.2.6)

где j - электростатический потенциал.

Представим электростатический потенциал j рядом Фурье вида (1.2.5)

(1.2.7)

Подставляя (1.2.7) в уравнение (1.2.6) и сравнивая с (1.2.5), приходим к соотношению, выражающему через структурные амплитуды F_hkl :

(1.2.8)

С учетом (1.2.8), ряд (1.2.7) принимает вид

(1.2.9)

Полученный ряд (1.2.9) сходится существенно быстрее, чем ряд (1.2.5).

Представим ряд (1.2.9) в интегральной форме. Будем использовать функцию Эвальда

(1.2.10)

Тогда выражение для потенциала j (x , y , z ) =j (R ) примет следующий вид:

(1.2.11)

где F(Н )– функция, достаточно хорошо сглаживающая значения структурных амплитуд в точках Н = H _hkl . Правая часть равенства (1.2.11) представляет собой преобразование Фурье произведения двух функций F ( H )/ H ² и Z (H ). Применяя к выражению (1.2.11) теорему о свертке функций, получим

, (1.2.12)

где функции f ( R ) и g ( R ) находятся Фурье-преобразованием функций F ( H )/ H ² и Z (H ).

Чтобы использовать выражение (1.2.12) для расчетов φ (x ,у ,z ),необходимо знать аналитический вид функции F (H ), которая на практике определена только в дискретных точках, где она имеет значение F_hkl . Для нахождения F (H ) воспользуемся методом аппроксимации. В качестве аппроксимирующей функции удобно взять следующее выражение:

, (1.2.13)

где z_i – число электронов на i -ой оболочке в атоме;

(1.2.14)

Для функции F (H ), данной выражением (1.2.13), может быть найдена функция f (R ), входящая в выражение для φ (х ,у ,z ) согласно (1.2.12). Эта функция находится Фурье-преобразованием выражения F (Н )/Н ² . В случае кубических решеток Фурье-преобразование может быть сведено к синус-преобразованию, тогда для f (R ) получим следующее выражение:

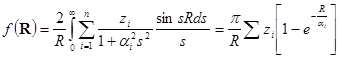(1.2.15)

Функция g (R ) является решеточной и находится Фурье-преобразованием Z (H ). В зависимости от количества атомов в элементарной ячейке производится вычисление g(R ), для лития она имеет вид:

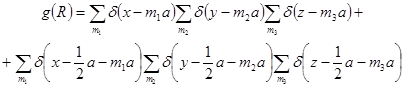(1.2.16)

где а — постоянная решетки; m ₁ , m ₂ , m ₃ — целые числа, начиная с нуля; δ (x -m ₁ a ), δ (y -m ₂ a ), δ (z -m ₃ a ) — δ -функции.

Совершив необходимые вычисления в (1.2.12), получаем следующее выражение для функции распределения потенциала:

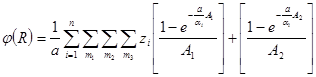, (1.2.17)