Дипломная работа: Расширение кольца с помощью полутела
3.Полукольцо S служит 0-расширением кольца с помощью полутела тогда и только тогда, когда идеал R ( S ) полульца S простой (т.е. ab Î R ( S ) влечет a Î R ( S ) или b Î R ( S )).
4.Для полукольца S с 1 фактор-полукольцо S / R ( S ) является полутелом с нулем тогда и только, когда R ( S ) есть максимальный односторонний идеал в S .
В качестве следствия утверждений 2 и 4 очевидным образом формулируется критерий разложимости полукольца с 1 в прямое произведение кольца и полутела с нулем. Отметим также, что подпрямые произведения кольца и ограниченной дистрибутивной решетки абстрактно охарактеризованы в [3].
5. Для существования 1-расширения полукольца K , возможно не имеющего нуля, с помощью полукольца T необходимо и достаточно, чтобы K имело 1, а T было идемпотентным полукольцом с 1.
6. Любое arp -полукольцо S является 1-расширением полутела U ( S ) с помощью ограниченной дистрибутивной решетки S /r , где r - конгруэнция на S , такая, что a r b означает aU ( S )= bU ( S ). Для коммутативных полуколец верно и обратное утверждение. См. [2].
7. Всякое полутело является 1-расширением сократимого полутела с помощью идемпотентного полутела [4].
Полукольцо S с 1 назовем 0-1-расширением полукольца K и полукольца без нуля L с помощью полукольца T , если на S существует такая конгруэнция r, что [0]ρ @K , [1]r @L и S /r @T .
Пусть для кольца R , полутела U и ограниченной дистрибутивной решетки L существует 0-1-расширение кольца R и полутела Uс помощью решетки L. Соответствующую тройку <R ,P ,L > будем называть допустимой .
§1. Допустимые кольца и решётки
Речь в главе пойдёт о решётке и кольце, состоящих в допустимой тройке.
Обозначим через D двухэлементную цепь.
Пусть имеется полукольцо S с конгруэнцией r , для которой [0]r @R , [1]r @P , F / r @D . Такое полукольцо S назовем дизъюнктным объединением кольца R и полутела P , и обозначим P ![]() R . Ясно, что "p Î P ,"r Î R ,p ×r Î R , p +r Î P .
R . Ясно, что "p Î P ,"r Î R ,p ×r Î R , p +r Î P .
С другой стороны, если любой элемент полукольца S с 1 либо обратим, либо имеет противоположный элемент, то S будет дизъюнктным объединением кольца R (S ) и полутела U (S ). При этом разбиение {R (S ), U (S )} индуцирует искомую конгруэнцию r на S .
Предложение. В U ![]() R справедливы следующие утверждения а) аддитивная группа R делимая абелева группа. б) результат умножения
R справедливы следующие утверждения а) аддитивная группа R делимая абелева группа. б) результат умножения ![]() определён единственным образом.
определён единственным образом.
Доказательство. а) Пусть ![]() , тогда
, тогда ![]() ,
, 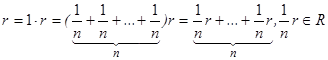 ч.т.д.
ч.т.д.
б) Пусть мультипликативная операция задана. Если ![]() , то
, то ![]() . Умножив равенство на
. Умножив равенство на ![]() справа, получим
справа, получим ![]() , значит
, значит ![]() . Рассмотрим результат умножения
. Рассмотрим результат умножения ![]() , пусть
, пусть ![]() . Тогда
. Тогда ![]() , поэтому
, поэтому ![]() есть элемент, складывая который
есть элемент, складывая который ![]() раз получим
раз получим ![]() . Из ранее доказанного следует, что такой элемент единственен, что завершает доказательство.
. Из ранее доказанного следует, что такой элемент единственен, что завершает доказательство. ![]() есть решение уравнения
есть решение уравнения ![]() в кольце
в кольце ![]() .
.
Теорема 1. Для произвольного кольца R эквивалентны следующие условия:
1) существует допустимая тройка áR , U , L ñ, где L – любая дистрибутивная решетка с 1 ¹ 0;
2) существует полукольцо, являющееся дизъюнктным объединением кольца R и полутела U ;
3) R – радикальное по Джекобсону кольцо, аддитивная группа которого есть делимая группа без кручения.
Доказательство.
1Þ2. Для данной тройки рассмотрим подходящие полукольцо S и конгруэнцию r . Поскольку D - подрешетка дистрибутивной решетки L с 0 и 1, в качестве дизъюнктного объединенияможно взять подполукольцо [1]r È[0]r в S .
2Þ1. Любая дистрибутивная решетка L обладает простым идеалом I , более того L \ I - дуальный идеал.
Поэтому в качестве полукольца S можно взять множество пар (i ,r ),i Î I ,r Î R È(l ,p ),l Î L / I ,p Î P с покоординатным сложением и умножением. Ввиду простоты I операции заданы корректно, аксиомы полукольца выполняются, поскольку они выполняются для левой координаты, как аксиомы решётки и для правой координаты, что следует из существования F , [0]r @R , [1]r @P , F / r @L 2 . Если в качестве конгруэнции g выбрать отношение равенства первых координат, то [0]g @R , [1]g @P , S / g @L 2 , что завершает доказательство.
Лемма. Пусть в кольце R "r $r ¢ "t Î R ,( r +r ¢ r + r ¢ ) t = 0Ù,( r +rr ¢ + r ¢ ) t = 0, тогда "r $r ² ,r +r ² r + r ² = 0Ùr +r ² r + r ² = 0.
Доказательство. Пусть выполнено условие леммы, тогда, положим r ² =- r - r ¢r . Имеем
r +r ² r +r ² = r +(- r - r ¢ r )r - r - r ¢ r = (r +r ¢ r +r ¢ )(-r )=0
r +rr ² +r ² = r +r (- r - r ¢ r ) - r - r ¢ r = (r +rr ¢ +r ¢ )(-r )=0.
Кольцо R называется радикальным по Джекобсону , если оно совпадает со своим радикалом Джекобсона (см., например, [5]). Это означает, что операция «круговой композиции» r °s = r +s +rs в R является групповой, с нейтральным элементом 0. Другими словами, в кольце R для любого элемента r существуетединственный элемент s , такой, что r +s +rs =0.
2)Þ3). P содержит Q + , иначе 1+ 1= 1, умножив равенство на ненулевой элемент кольца r , имеем r + r = r Ûr =0 – противоречие. Таким образом, R – полумодуль над Q + и, значит, модуль над Q . Поэтому <R ,+ > - делимая абелева группа без кручения (подробно см. также предложение).
Множество T=Q + + R является подполутелом в U , поскольку
q 1 + r 1 + q 2 + r 2 = (q 1 + q 2 )+ (r 1 + r 2 );
(q 1 + r 1 )(q 2 + r 2 ) = (q 1 q 2 + q 1 r 2 + r 1 q 2 + r 1 r 2 ) = q 1 q 2 + (q 1 r 2 + r 1 q 2 + r 1 r 2 );
t=q+r Þ1=qt -1 +rt -1 Þt -1 =q -1 - q -1 r t -1 Î Q+ + R.
Следовательно, для любого элемента 1+r ,r Î R найдётся, 1+r ¢ ,r ¢ Î R что (1+r )(1+r ¢ ) = (1+r ¢ )(1+r ) = 1. Из дистрибутивности следует, что 1+r +rr ¢ +r ¢ = 1+r +r ¢ r +r ¢ = 1. Умножая последнее равенство на любое t Î R , имеем (r +r ¢ r + r ¢ )t = 0Ù(r +rr ¢ + r ¢ )t = 0, значит, в виду леммы, R радикально по Джекобсону.