Метод единичной ячейки, рассмотренный в [7], применяется для анализа больших АР, состоящих из идентичных излучателей, возбуждаемых с одинаковой амплитудой и одинаковой разностью фаз между соседними элементами. Суть метода заключается в том, что все пространство АР делится две части: нижнюю, где помещается система питания, и верхнюю, в которую решетка излучает. В верхней части вокруг одного из излучателей образуют единичную ячейку, состоящую из двух электрических и двух магнитных стенок, простирающихся до бесконечности. Стенки располагают таким образом, чтобы выполнялись граничные условия и тем самым не нарушалась структура поля, сформированного под воздействием взаимного влияния элементов. После введения стенок можно пренебречь полем вне единичной ячейки, а саму ячейку можно рассматривать как своего рода волновод. Все взаимные связи между щелями учитываются автоматически. Такой подход позволяет использовать хорошо развитую теорию волноводов.

2 . Расчет полевых и импедансных характеристик ФАР

Результаты, полученные на основе модели бесконечных периодических структур, позволяют оценить свойства центральных излучателей больших АР. Часто требуется выполнить расчеты для АР малых размеров, либо исследовать краевые эффекты в больших АР. Расчет взаимных сопротивлений можно выполнять и методами поэлементного подхода, но как правило это сложная электродинамическая задача. Решить данную задачу позволяет процедура, построенная на основе эквивалентности метода поэлементного расчета входных сопротивлений излучателя в бесконечной АР и метода, основанного на теории бесконечных периодических структур [2 ].

2.1 Входное сопротивление элемента бесконечной периодической линейной решетки

Для линейной решетки полосковых вибраторов, расположенных на многослойной диэлектрической подлжке (рис. 2.1) и имеющих распределение тока

, (2.1 )

где -единичный вектор, входное сопротивление можно записать в виде [1]

, (2.2 )

где J(y) – распределение тока по (2.1);

- скалярная компонента функции Грина при разложении полей по волнам Е и Н.

, (2.3 )

где - собственные функции [1];

-характеристические части функции Грина.

Записав выражения для характеристических частей и собственных функций и подставив их в (2.2) и (2.3), получим выражение для расчета входного сопротивления вибратора, имеющего структуру как на рис. 2.1 и находящегося в составе бесконечной решетки с периодом B [1]

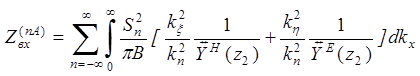, ( 2.4)

где B=nA – период решетки;

- множитель, учитывающий распределение тока по вибратору;

;

;

;

;

α – угол наклона излучателей в решетке (α=0° – параллельные излучатели, α=90° – коллинеарные излучатели).

Для слоистой структуры, представленной на рис. 2.1, проводимость в сечении определяется по следующим рекурентным формулам:

;

;

;

;

; ;

; ; .

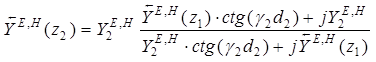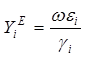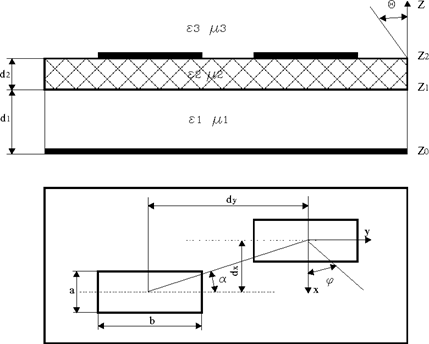
Рис. 2.1 Геометрия полосковых излучателей на многослойной диэлектрической подложке