Дипломная работа: Рекурсия

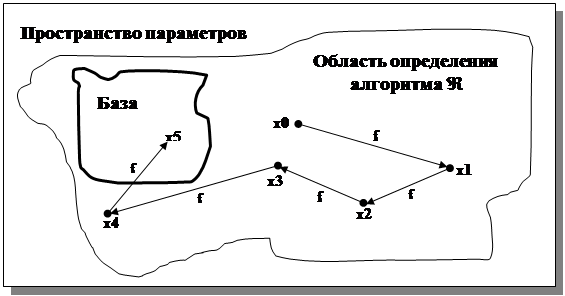
Таблица 3.1. Схематическое изображение последовательности рекур-

сивных обращений и формирования полной рекурсивной траектории

В оставшейся части данного пункта рассматривается серия простых учебных демонстрационных задач, решения которых получаются с помощью рекурсивно определенных алгоритмов. Во многих случаях детально обсуждаются описанные выше схематические приемы поиска этих алгоритмов. В основном все программы-функции написаны на языке программирования вычислительной среды Mathcad. Часть программ написана на языке ObjectPascal 5.0 системы объектного визуального программирования Delphi 5. Для некоторых задач предлагается несколько вариантов программ. Приводятся контрольные примеры. Заметим, что, ввиду разноплановости предложенных задач, многие из них могут служить отдельными темами, собирающими вокруг себя родственный содержательный материал по рекурсии для отработки техники рекурсивного программирования в рамках конкретного направления.

Результатом проработки материала данного пункта должно стать убеждение, что писать рекурсивные программы, как правило, несложно, а получаемые при этом тексты весьма компактны и, по причине отсутствия в них диких зарослей языковых украшательств, легко читаются. Нам представляется, что читатель вряд ли откажет себе в удовольствии написать собственные программы-функции решения многих из приведенных задач или их обобщений.

3.1 Факториал

Задача 1. Составить программу-функцию вычисления факториала целого неотрицательного числа n.

Решение. Для целых неотрицательных чисел nфакториал n обозначается через n! и определяется так:

В данном случае параметризация задачи осуществлена в её постановке. Остается лишь ввести более приемлемое для нас обозначение искомой функции. Пусть это будет facto(n). Тривиальные случаи, для которых задача решается без рекурсивных вызовов, также очевидны: facto(0)=1, facto(1)=1. Они и составляют базу рекурсии. Декомпозиция по параметру n реализуется по формуле: facto(n) = n×facto(n–1) (n = 1, 2, …). Поэтому вычисления facto(n) можно организовать так:

Контрольные примеры.

Понять процесс реализации рекурсивных вызовов, то есть декомпозицию, и возвратов управления при организации отложенных вычислений facto(n) можно из схемы рис. 3.1 (n = 3). Там около стрелок в круглых скобках жирными цифрами указаны номера последовательных шагов вычислений: (1 ), (2 ), (3 ) - декомпозиция; (4 ), (5 ), (6 ) - отложенные вычисления.

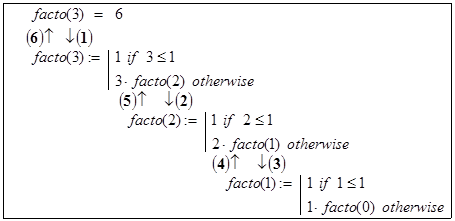
Рис. 3.1. Схематическое изображение рекурсивных вызовов и

отложенных вычислений при нахождении facto(3) = 3!.

Замечание. С помощью встроенной функции if() предложенный алгоритм удается записать еще короче. Это же касается и многих других примеров.

Для решения конкретной задачи иногда удается построить несколько различных рекурсивных алгоритмов. Например, функцию facto(n) можно было бы определить и так.

По сравнению с прежней реализацией facto() здесь количество рекурсивных вызовов уменьшается практически в 2 раза. В реальных ситуациях подобный фактор может оказаться решающим при выборе того или иного алгоритма.

Используем теперь для вычисления n! cформулированную выше схему 3 (обобщить). Если вместо исходной функции facto(n)=n!, ввести в рассмотрение функцию двух переменных fa(n, l)=l×n! (n=0,1,…), то получим равенства:

fa(n, l)=l×n×(n-1)×…×1=(l×n)×(n-1)!=fa(l×n)×(n-1)!,

fa(1, l)=l , fa(n,1)=n!.

Первое из этих соотношений может служить правилом декомпозиции, второе - определять рекурсивную базу, а третье - показывает, как вычислять n!. Соответствующая рекурсивная программа-функция могла бы выглядеть так:

В чем же отличие этой функции от первого варианта функции facto(n)? Дело в том, в facto(n) формирование n! реализуется при проведении отложенных вычислений, в то же время нахождение fa(n,l) проводится вообще без отложенных вычислений. Особенно наглядно это видно на рисунках 3.1 и 3.2. На шагах 4, 5 и 6, отмеченных на рис. 3.2 жирными цифрами в круглых скобках, происходит лишь передача значений. Иными словами здесь мы имеем повторительную рекурсию.

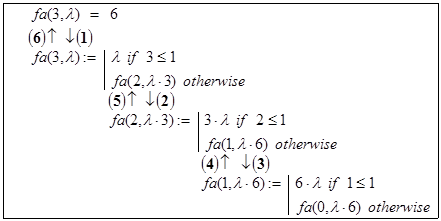
Рис. 3.2. Схематическое изображение рекурсивных вызовов