Дипломная работа: Рекурсия

Еще один вариант вычисления n! можно реализовать с помощью рассмотренной ниже в задаче 20 функции Кадью.

3.2 Сложный процент

Задача 2. Вкладчик положил в сбербанк сумму в sum единиц под p процентов за один период времени (год, месяц, неделя и т.д.). Составить программу-функцию возвращающую величину вклада по истечении n периодов времени (n = 1, 2,).

Решение. Пусть invest(sum,p,n) искомая функция. Для данной задачи вычисления значений invest() можно проводить по формуле

invest(sum,p,n) = sum×(1+p/100)ⁿ .

Однако, в учебных целях, нас интересует рекурсивный вариант алгоритма решения задачи. Рекурсию будем осуществлять по параметру n. Тривиальный случай очевиден. Если вклад положен на хранение и взят сразу, то есть до истечения первого периода времени начисления процентов, то возврату подлежит начальная сумма вклада - sum. Далее, декомпозиция может быть реализована исходя из следующего факта. Положить некоторую сумму в банк на n периодов – это то же самое, что положить эту сумму на n – 1 периодов и затем полученную сумму положить на 1 период. Соответствующий вариант программы-функции решения задачи выглядит так:

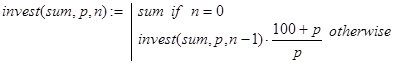
Контрольные примеры.

Схема рекурсивных вызовов здесь такая же, как при вычислении значений функции facto(n). Нетрудно видеть, что общее количество рекурсивных вызовов при вычислении invest(sum,p,n) равно n. При необходимости можно было бы уменьшить это значение до log₂ (n).

3.3 Степень числа

Задача 3. Пусть a- вещественное число отличное от нуля и n- целое неотрицательное число. Составить программу-функцию возвращающую величину aⁿ .

Решение. Приведенная ниже функция power(a,n) дает решение задачи за n рекурсивных вызовов:

Уменьшить количество вызовов можно так. Организуем декомпозицию иначе, представив величину aⁿ в виде:

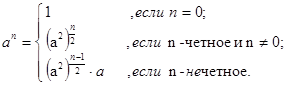
Отсюда сразу же получаем алгоритм вычисления aⁿ , требующий не более log₂ (n) рекурсивных вызовов. Реализуется он функцией pow(a,n):

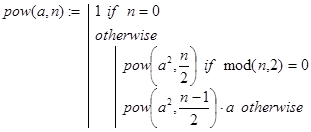
Сумма элементов массива

Задача 4. Составить программу-функцию, возвращающую сумму S компонентов вектора v=(a₀ ,a₁ ,…,a_{n - 1} )^T : S= a₀ +a₁ +…+a_{n - 1} , где n³1 и a_p (p=0..n-1) - вещественные или комплексные числа.

Решение. Определение суммы n слагаемых в виде:

S= a₀ +a₁ +…+a_{n - 1} =(a₀ +a₁ +…+a_{n - 2} )+a_{n - 1}

рекурсивно по своей сути. Сумма n слагаемых есть сумма первых (n-1)-го слагаемого плюс сумма последнего слагаемого. Этот факт и положен в основу определения функции summa(v), где v=(a₀ ,a₁ ,…,a_{n - 1} )^T .

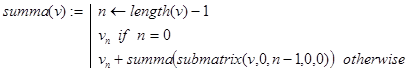
3.4 Произведение элементов массива

Задача 5. Составить программу-функцию, возвращающую произведение P компонентов вектора v=(a₀ ,a₁ ,…,a_{n - 1} )^T : P= a₀ ×a₁ ×…×a_{n - 1} , где n³1 и a_p (p=0..n-1) - вещественные или комплексные числа.

Решение. Определение произведения n сомножителей в виде:

P= a₀ ×a₁ ×…×a_{n - 1} = (a₀ ×a₁ ×…×a_{n - 2} )×a_{n - 1} ,

как и соответствующее определение суммы, рекурсивно по своей сути. Произведение n сомножителей есть произведение первых (n-1)-го сомножителей умноженное на последний сомножитель. Отсюда и определение функции product(v), где v=(a₀ ,a₁ ,…,a_{n - 1} )^T .

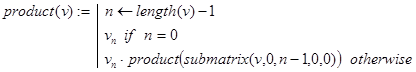
3.5 Числа Фибоначчи

Задача 6. Составить программу-функцию вычисления n-го числа Фибоначчи, исходя из рекуррентного определения этих чисел:

f(0)=f(1)=1, f(n)=f(n-1)+f(n-2) (n=2,3,…).(1)