Дипломная работа: Решение транспортной задачи линейного программирования в среде MS Excel

При рассмотрении задач линейного программирования, следует помнить что, с одной стороны, они являются специальным случаем общей задачи оптимизации. Тем самым для задач линейного программирования оказываются справедливыми соответствующие результаты относительно общих свойств и способов их решения, разработанные в теории решения экстремальных задач. С другой стороны, специальная форма задания целевой функции и ограничений в форме линейных функций приводит к появлению у данного класса задач целого ряда специальных свойств, которые послужили основой разработки специализированных методов и алгоритмов их решения. Для детального анализа этих специальных свойств следует рассмотреть общую математическую постановку задачи линейного программирования.

1.2 Математическая постановка задачи линейного

программирования

В общем случае математическая постановка задачи линейного программирования, может быть сформулирована в следующем виде:

f(x1,x2…,,x n)® где (1.1)

x1,x2…,,x n (1.2)

(k{1,2,…,m}).

при этом следует принимать во внимание следующие принципиальные предположения о характере целевой функции и левых частей ограничений:

1. Целевая функция f(x1,x2…,,x n ) предполагается линейной относительно всех своих переменных, т.е. может быть представлена в форме всех своих представлена в форме: f(x1,x…,,x n)=с1х1+с2х2+…+с n x n.

2. Левые части ограничений g k(x1,x2…,,x n) ({1,2,…,m}) также является линейными функциями относительно своих переменных x1,x2…,,x n, т.е. могут быть представлены в форме: g k(x1,x2…,,x n)=ак1х+ак2х2+…+а к n x n.

3. Переменные x1,x2…,,x n могут принимать свои значения только из множество неотрицательных действительных чисел R1+ ,т.е. хi R1+ ({1,2,…,n}).

С учетом сделанных предположений общая задача линейного программирования может быть сформулирована следующим образом.

Необходимо найти максимум линейной целевой функции n переменных x1,x2…,,x n R1+ следующего вида:

с1х1+с2х2+…+с n x n ® (1.3)

где множество допустимых альтернатив формируется следующей системой ограничений типа равенств и неравенств:

аi1х+аi2х2+…+а in x n=bi ({1,2,…,q}). (1.4)

ак1х+ак2х2+…+а к n x n.bk ({q+1,2,…,m}). (1.5)

В математической постановке общей задачи линейного программирования через сi, aki , bk ({1,2,…,n}),({1,2,…,m}) обозначены постоянные величины, которые могут принимать произвольные, не обязательно целочисленные значения, определяемые спецификой конкретной задачи линейного программирования.

В случае отсутствия ограничений типа равенств (1.4), т.е. при q=0, задача линейного программирования называется стандартной задачей линейного программирования, которая, с учетом сделанных предположений, может быть записана в следующем виде:

с1х1+с2х2+…+с n x n ® (1.6)

где множество допустимых альтернатив формируется следующей системой ограничений типа неравенств:

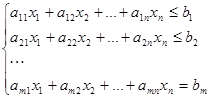(1.7)

и x1,x2…,,x n 0

С другой стороны, при отсутствии ограничений типа неравенств (1.5), т.е. при q=m, задача линейного программирования называется канонической или основной задачей линейного программирования, которая с учетом сделанных предположений, может быть записана в следующем виде:

с1х1+с2х2+…+с n x n ® (1.8)

где множество допустимых альтернатив формируется следующей системой ограничений типа неравенств:

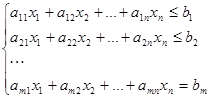(1.9)

и x1,x2…,,x n 0.

При рассмотрении общих особенностей задачи линейного программирования удобной оказывается стандартная форма математической постановки задачи линейного программирования (1.6) и (1.7). Анализ множества допустимых альтернатив стандартной задачи линейного программирования (1.6) и (1.7) позволяет прийти к выводу о справедливости только одной из трех возможных ситуаций:

1. Система ограничений (1.7) противоречива или несовместна, т.е. не существует ни одного выбора значений x1,x2…,,x которые удовлетворяют ограничениям (1.7). В этом случае задача линейного программирования не имеет решения.

2. Система ограничений (1.7) не является противоречивой, однако соответствующая ей область пространства R n является неограниченной. В этом случае задача линейного программирования не имеет решения, в случае, если линейная функция (1.6) не ограничена в неограниченной области, соответствующей множеству допустимых альтернатив .