Дипломная работа: Решение транспортной задачи линейного программирования в среде MS Excel

6. Скопируем формулу, введенную в ячейку F6, в ячейки F7 и F8.

7. В ячейку В9 введем формулу: =сумм (В6:В8), которая представляет четвертое ограничение (2.7).

8. Скопируем формулу, введенную в ячейку В9, в ячейки C9, D9 и E9.

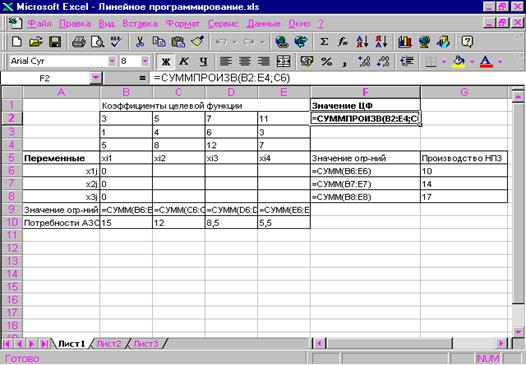
Внешний вид рабочего листа MS Office Excel с исходными данными для решения транспортной задачи показан на рисунке 2.1.

Для дальнейшего решения задачи следует вызвать мастер поиска решения, для чего необходимо выполнить операцию главного меню: Сервис│Поиск решения…

После появления диалогового окна Поиск решения следует выполнить следующие действия:

1.В поле с именем Установить целевую ячейку: ввести абсолютный

адрес ячейки $F$2.

2.Для группы Равной: выбрать вариант поиска решения- минимальному значению.

Рисунок. 2.1 Исходные данные для решения

транспортной задач

3. В поле с именем Изменяя ячейки: ввести абсолютный адрес диапазона ячеек $B$2:$E$4.

4.Добавить 7 ограничений, соответствующих базовым ограничениям исходной постановки решаемой транспортной задачи. С этой целью выполнить следующие действия:

· для задания первого ограничения в исходном диалоговом окне Поиск решения нажать кнопку с надписью Добавить;

· в появившемся дополнительном окне выбрать ячейку $F$6, которая

должна отобразиться в поле с именем Ссылка на ячейку;

· в качестве знака ограничений из выпадающего списка выбрать строгое неравенство “=”;

· в качестве значения правой части ограничения выбрать ячейку $С$6;

· для добавления первого ограничения в дополнительном окне нажать кнопку с надписью Добавить;

· аналогичным образом задать оставшиеся 6 ограничений.

5.Добавить последнее ограничение на неотрицательность значений переменных задачи. Внешний вид диалогового окна мастера поиска решения с ограничениями для транспортной задачи изображен на рисунке 2.2.

6.В дополнительном окне параметров поиска решения следует выбрать отметки Линейная модель и Неотрицательные значения.

Рисунок 2.2. Параметры мастера поиска решения и базовых

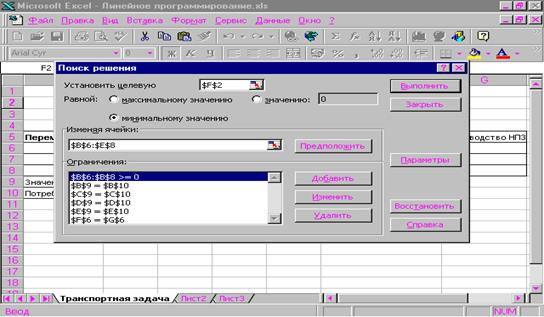ограничения для транспортной задачи

После задания ограничений и целевой функции можно приступить к поиску численного решения, для чего следует нажать кнопку Выполнить. После выполнения расчетов программой MS Excel будет получено количественное решение, которое имеет следующий вид рисунок 2.3.

Рисунок 2.3 Результат количественного

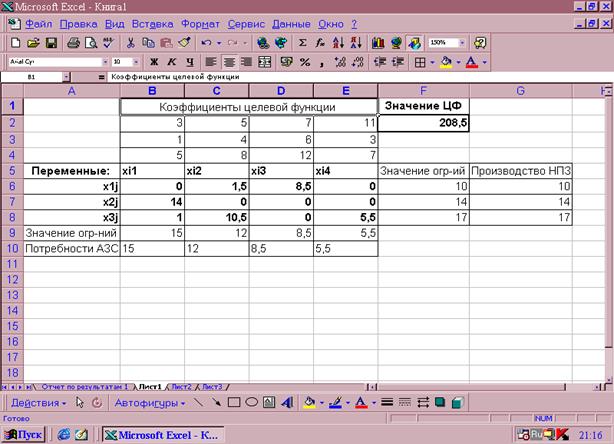решения транспортной задачи

Результатом решения транспортной задачи являются найденные оптимальные значения переменных: х11=0, х12=1,5, х13=8,5, х14=0, х21=14, х22=0, х23=0, х24=0, х31=1, х32=10,5, х33=0, х34=5,5, которым соответствует значение целевой функции: f opt = 208,5. При выполнении расчетов для ячеек В6:Е8 был выбран числовой формат с тремя знаками после запятой.

Анализ найденного решения показывает, что для удовлетворения потребностей АЗС №1 следует транспортировать 14т бензина из НПЗ №2 и 1т- из НПЗ №3, для удовлетворения потребностей АЗС №2 следует транспортировать 1,5 т бензина из НПЗ №1 и 10,5т – из НПЗ №3, для удовлетворения потребностей АЗС №3 следует транспортировать 8,5 т бензина из НПЗ №1 и, наконец, для удовлетворения потребностей АЗС №4 следует транспортировать 5,5 т бензина из НПЗ №3. При этом общая стоимость найденного плана перевозок составит 208,5 тысяч тенге.