Дипломная работа: Схема Бернулли. Цепи Маркова

Рассмотрим схему Бернулли с вероятностью успеха в одном испытании. Введем величину со значениями равную номеру первого успешного испытания.

Теорема 2. Вероятность того, что первый успех произойдет в испытании с номером равна

.

Доказательство. Вероятность первым испытаниям завершиться неудачей, а последнему - успехом, равна

Определение 3. Набор чисел называется геометрическим распределением вероятностей.

Геометрическое распределение вероятностей обладает интересным свойством, которое можно назвать свойством "нестарения".

Теорема 3. Пусть для любого . Тогда для любых неотрицательных целых и имеет место равенство:

Если, например, считать величину временем безотказной работы (измеряемым целым числом часов) некоторого устройства, то данному равенству можно придать следующее звучание: вероятность работающему устройству проработать еще сколько-то часов не зависит от того момента, когда мы начали отсчет времени, или от того, сколько уже работает устройство. Общепринятое название этого свойства - свойство отсутствия последействия.

Доказательство. По определению условной вероятности,

(1)

Последнее равенство следует из того, что событие влечет событие поэтому пересечение этих событий есть . Найдем для целого вероятность :

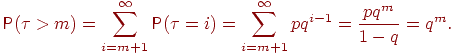
Можно получить еще проще: событие означает в точности, что в схеме Бернулли первые испытаний завершились неудачами, т.е. его вероятность равна . Возвращаясь к (1), получим

Теорема 3 доказана.

1.2.2 Независимые испытания с несколькими исходами

Рассмотрим схему независимых испытаний уже не с двумя, а с большим количеством возможных результатов в каждом испытании.

Пример 1. Игральная кость подбрасывается 15 раз. Найти вероятность того, что выпадет ровно десять троек и три единицы.

Здесь каждое испытание имеет три, а не два исхода: выпадение тройки, выпадение единицы, выпадение любой другой грани. Поэтому воспользоваться формулой для числа успехов в схеме Бернулли не удаcтся.

Попробуем вывести подходящую формулу. Пусть в одном испытании возможны исходов: , и -й исход в одном испытании случается с вероятностью , где .

Обозначим через вероятность того, что в независимых испытаниях первый исход случится раз, второй исход - раз, и т.д., наконец, -й исход - раз.

Теорема 4 (Обобщенная формула Бернулли). Для любого и любых неотрицательных целых чисел сумма которых равна верна формула

Доказательство. Рассмотрим один элементарный исход, благоприятствующий выпадению единиц, двоек и т.д.:

Это результат экспериментов, когда все нужные исходы появились в некотором заранее заданном порядке. Вероятность такого результата равна произведению вероятностей . Остальные благоприятные исходы отличаются лишь расположением чисел на местах. Число таких исходов равно числу способов расположить на местах единиц, двоек, и т.д. Это число равно

Теперь мы можем вернуться к примеру 1 и выписать ответ: вероятность получить десять троек, три единицы и еще два других очка равна