Дипломная работа: Схема Бернулли. Цепи Маркова

так как вероятности выпадения тройки и единицы равны по , а вероятность третьего исхода (выпала любая другая грань) равна

1.2.3 Теорема Пуассона для схемы Бернулли

Предположим, нам нужна вероятность получить не менее семи успехов в тысяче испытаний схемы Бернулли с вероятностью успеха . Вероятность этого события равна любому из следующих выражений, вычислить которые довольно сложно:

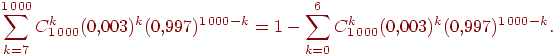
Сформулируем теорему о приближенном вычислении вероятности иметь успехов в большом числе испытаний Бернулли с маленькой вероятностью успеха . Термин "большое число" должен означать . Если при этом остается неизменной, то вероятность получить любое заданное число успехов уменьшается до нуля. Необходимо чтобы вероятность успеха уменьшалась одновременно с ростом числа испытаний. Но от испытания к испытанию вероятность успеха меняться не может (см. определение схемы Бернулли). Поэтому нам придется рассмотреть так называемую "схему серий": если испытание одно, то вероятность успеха в нем равна если испытаний два, то вероятность успеха в каждом равна и т.д. Если испытаний то в каждом из них вероятность успеха равна . Вероятность успеха меняется не внутри одной серии испытаний, а от серии к серии, когда меняется общее число испытаний. Обозначим через число успехов в -й серии испытаний.

Теорема 5 (теорема Пуассона). Пусть и так, что Тогда для любого вероятность получить успехов в испытаниях схемы Бернулли с вероятностью успеха стремится к величине

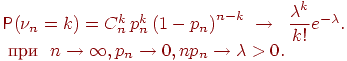
Доказательство. Положим . По условию . Подставим в формулу Бернулли:

(2)

В соотношении (2) мы воспользовались тем, что и замечательным пределом . Докажем последнее свойство:

Определение 4. Набор чисел называется распределением Пуассона с параметром .

По теореме 17 можно приближенно посчитать вероятность получить не менее семи успехов в тысяче испытаний схемы Бернулли с вероятностью успеха с вычисления которой мы начали. Поскольку "велико", а "мало", то, взяв можно записать приближенное равенство

(3)

Осталось решить, а достаточно ли велико, а мало, чтобы заменить точную вероятность на ее приближенное значение. Для этого нужно уметь оценивать разницу между этими вероятностями.

Следующую очень полезную теорему мы, исключительно из экономии времени, доказывать не станем.

Теорема 6 (уточненная теорема Пуассона). Пусть - произвольное множество целых неотрицательных чисел, - число успехов в испытаниях схемы Бернулли с вероятностью успеха . Cправедливо неравенство

Таким образом, теорема 6 предоставляет нам возможность самим решать, достаточно ли велико, а мало, руководствуясь полученной величиной погрешности. Какова же погрешность в формуле (3)? Взяв имеем

Таким образом, можно утверждать, что искомая вероятность заключена в границах .

Пример 2. В урне 20 белых и 10 черных шаров. Вынули 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Найти вероятность того, что из четырех вынутых шаров окажется 2 белых.

Решение. Событие А – достали белый шар. Тогда вероятности, . По формуле Бернулли требуемая вероятность равна

.

Пример 3. Определить вероятность того, что в семье, имеющей 5 деталей, будет не больше трех девочек. Вероятности рождения мальчика и девочки предполагаются одинаковыми.

Решение. Вероятность рождения девочки , тогда .

Найдем вероятности того, что в семье нет девочек, родилась одна, две или три девочки:

, ,

, .

Следовательно, искомая вероятность