Определение 1. Отображением множества M на множество N называется правило f, которое каждому элементу m из множества M ставит в соответствие элемент n из множества N, называемый образом элемента m, при этом каждый элемент множества N является образом хотя бы одного элемента из множества M.
Если M=N, то говорят об отображении множества М на себя.
Определение 2. Операцией симметрии конечной фигуры называется ее изомерическое (т. е. сохраняющее расстояние между точками фигуры) отображение на себя.
Рассматривая эти примеры, приходим к заключению, что помимо геометрической модели, с молекулой аммиака необходимо связать геометрические образы – прямую C3 и плоскость  , которые не принадлежат модели хотя бы потому, что они бесконечны
, которые не принадлежат модели хотя бы потому, что они бесконечны
Операции симметрии пространственной фигуры, соответствующей молекуле, называются операциями симметрии молекулы.





? ???????? ??????? ?????????? ???????? ??????? NH
3 . ?? ?????????????? ???????????? ????? ????? ?????????? ???????????
???. 1 ????????.
К числу операций симметрии правильной треугольной пирамиды относятся повороты, совмещающие ее с собой. Точки N и O определяют ось поворота, которую обозначим через С3 . Повернем пирамиду вокруг этой оси на 120о против часовой стрелки. Указанный поворот обозначим через  . На рис. 1, б изображена фигура (результат поворота), которая совмещается с исходной (рис. 1, а) при наложении. Рассмотрим отражение в плоскости
. На рис. 1, б изображена фигура (результат поворота), которая совмещается с исходной (рис. 1, а) при наложении. Рассмотрим отражение в плоскости  , совмещающее фигуру с собой, и обозначим его
, совмещающее фигуру с собой, и обозначим его  . Очевидно, что
. Очевидно, что  , как и
, как и  , является операцией симметрии молекулы аммиака, так как операции
, является операцией симметрии молекулы аммиака, так как операции  и
и  не изменяют расстояний между точками фигуры NH3 .
не изменяют расстояний между точками фигуры NH3 .
Рассматривая эти примеры, приходим к заключению, что помимо геометрической модели, с молекулой аммиака необходимо связать геометрические образы – прямую C3 и плоскость  , которые не принадлежат модели хотя бы потому, что они бесконечны.
, которые не принадлежат модели хотя бы потому, что они бесконечны.
Определение 3. Элементом симметрии молекулы называется вспомогательный геометрический образ (точка, прямая, плоскость), характеризующий некоторое множество операций симметрии фигуры, изображающей молекулу.
Например, ось C3 характеризует множество операций симметрии, состоящее из рассмотренного нами поворота  , а также поворотов
, а также поворотов  на 240о и
на 240о и  на 360о против часовой стрелки молекулы аммиака. Поворот
на 360о против часовой стрелки молекулы аммиака. Поворот  называется тождественной операцией симметрии. При этой операции симметрии все точки геометрической модели молекулы отображаются в себя. Плоскость
называется тождественной операцией симметрии. При этой операции симметрии все точки геометрической модели молекулы отображаются в себя. Плоскость  характеризует множество операций симметрии, состоящее из
характеризует множество операций симметрии, состоящее из  и
и  .
.
Элементы симметрии не следует путать с операциями симметрии. Элементы симметрии будем обозначать буквами, а операции симметрии – буквами «со шляпками» над ними.
Рассмотрим множество, элементами которого являются всевозможные операции симметрии молекулы, для случая молекулы аммиака. Четыре элемента  ,
,  ,
,  ,
,  этого множества мы уже нашли. Кроме плоскости
этого множества мы уже нашли. Кроме плоскости  (рис. 1, а), молекула аммиака имеет еще две плоскости симметрии
(рис. 1, а), молекула аммиака имеет еще две плоскости симметрии  и
и 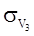 , содержащие прямые NH(2) и NH(3) соответственно. С плоскостями
, содержащие прямые NH(2) и NH(3) соответственно. С плоскостями  и
и 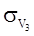 связаны операции симметрии
связаны операции симметрии 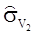 и
и 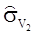 . Множество операций симметрии молекулы аммиака может быть обозначено следующим образом:
. Множество операций симметрии молекулы аммиака может быть обозначено следующим образом:
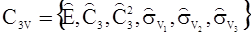 .
.
2. Классификация элементов симметрии молекулы
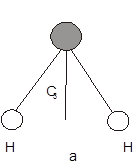
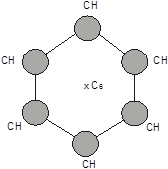
1. Поворотная ось Cn порядка n. Поворотной осью симметрии n-го порядка называется ось Cn , при повороте вокруг которой на угол a=2p/n молекула совмещается сама с собой. Примеры: C3 – для случая молекулы аммиака; C2 (рис. 2, а) – для случая молекулы воды; C6 – для случая молекулы бензола (рис. 2, б).
2. Поворотная ось бесконечного порядка C ¥ . Это поворотная ось, при повороте вокруг которой на любой угол молекула совмещается с собой. Примером может служить любая линейная молекула, например, молекула ацетилена C2 H2 (рис. 3).
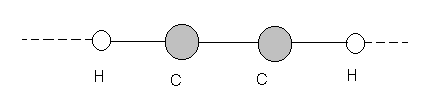
Рис. 2
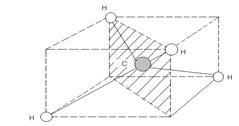
Рис. 3
3. Плоскость симметрии. ?????????? ????????? ???????? ?????????? ?????????, ??? ????????? ? ??????? ???????? ??????????? ???? ? ?????. ?????? ???????? ? ???????????? ?????????? ????????? ??? ???????? (???????? ???????). ? ??????? C
6 H
6 (???. 2, ?) ???? ????????? ?????????
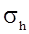
- ?????????, ? ??????? ????? ????? ???? ????????. ??? ???? ??????? ????? ?????, ??? ?????????? ??? ??????? ??????? ?????? ??????? ??????????? ?? ????????????.
Диагональную плоскость симметрии имеет молекула метана (рис. 4). Геометрической моделью CH4 является тетраэдр, в вершине которого расположены атомы водорода. Диагональная плоскость симметрии sd заштрихована. При отражении в плоскости sd атомы водорода, находящиеся в плоскости, переходят в себя, а атомы, расположенные симметрично этой плоскости, переходят друг в друга.
4. Центр симметрии. Это точка i, при отражении в которой молекула совмещается сама с собой, например, молекула трансдихлорэтилена C2 Cl2 H2 (рис. 5).
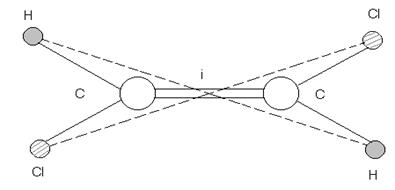
Рис. 5
5. Зеркально-поворотная ось n-го порядка Sn . Зеркально-поворотной осью n-го порядка называется ось, при повороте вокруг которой на угол a=2p/n с последующим
?????????? ? ?????????, ???????????????? ? ???? ???, ???????? ??????????? ???? ? ?????.
???????? ???????, ?????????? ????? ????, ????? ??????? ???????? ?????? CH
4 .
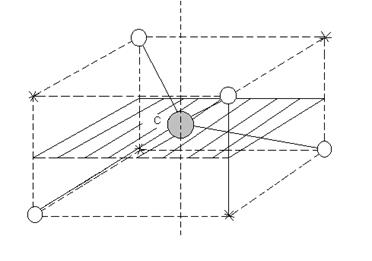
Рис. 6
?? ???. 6 ???????? ?????????-?????????? ??? ????????? ?????????? ??????? S
4 . ?? ???. 6 ????? ??????, ??? ??? ???????? ?? ???? a=2p/4 ?????? ??? S
4 ?????? ??????? ??????? ????? H
( i) ????????? ? ?????, ????????? ???????????. ???????? ????? ????-
????? ? ?????????????? ?????????????? ?????????, ???????, ??? ??? ????????? ???????? ? ??????????????? ?????, ?. ?. ? ?????????? ??????????? ???????? S
4 ???? H
(1) ???????? ? H
(3) , H
(2) ? ? H
(4) , H
(3) ? ? H
(2) , H
(4) ? ? H
(1) .
1.2 Групповые постулаты
1. Алгебраические операции
Определение 1. Бинарной алгебраической операцией, определенной на множестве М, называется правило, согласно которому каждые два элемента a и b множества М, взятые в определенном порядке, однозначно сопоставляются с элементом с из этого множества, называемым результатом выполнения операции.
Рассмотрим в качестве общего примера множество операций симметрии молекулы. Под произведением операций симметрии 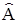 и
и 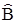 будем понимать их последовательное выполнение. Первые два требования к алгебраической операции, очевидно, выполняются. Проверим выполнение третьего условия из определения алгебраической операции.
будем понимать их последовательное выполнение. Первые два требования к алгебраической операции, очевидно, выполняются. Проверим выполнение третьего условия из определения алгебраической операции.
![]() , которые не принадлежат модели хотя бы потому, что они бесконечны
, которые не принадлежат модели хотя бы потому, что они бесконечны

![]() . На рис. 1, б изображена фигура (результат поворота), которая совмещается с исходной (рис. 1, а) при наложении. Рассмотрим отражение в плоскости
. На рис. 1, б изображена фигура (результат поворота), которая совмещается с исходной (рис. 1, а) при наложении. Рассмотрим отражение в плоскости ![]() , совмещающее фигуру с собой, и обозначим его
, совмещающее фигуру с собой, и обозначим его ![]() . Очевидно, что
. Очевидно, что ![]() , как и
, как и ![]() , является операцией симметрии молекулы аммиака, так как операции
, является операцией симметрии молекулы аммиака, так как операции ![]() и
и ![]() не изменяют расстояний между точками фигуры NH3 .
не изменяют расстояний между точками фигуры NH3 . ![]() , которые не принадлежат модели хотя бы потому, что они бесконечны.
, которые не принадлежат модели хотя бы потому, что они бесконечны. ![]() , а также поворотов
, а также поворотов ![]() на 240о и
на 240о и ![]() на 360о против часовой стрелки молекулы аммиака. Поворот
на 360о против часовой стрелки молекулы аммиака. Поворот ![]() называется тождественной операцией симметрии. При этой операции симметрии все точки геометрической модели молекулы отображаются в себя. Плоскость
называется тождественной операцией симметрии. При этой операции симметрии все точки геометрической модели молекулы отображаются в себя. Плоскость ![]() характеризует множество операций симметрии, состоящее из
характеризует множество операций симметрии, состоящее из ![]() и
и ![]() .
.![]() ,
, ![]() ,
, ![]() ,
, ![]() этого множества мы уже нашли. Кроме плоскости
этого множества мы уже нашли. Кроме плоскости ![]() (рис. 1, а), молекула аммиака имеет еще две плоскости симметрии
(рис. 1, а), молекула аммиака имеет еще две плоскости симметрии ![]() и
и ![]() , содержащие прямые NH(2) и NH(3) соответственно. С плоскостями
, содержащие прямые NH(2) и NH(3) соответственно. С плоскостями ![]() и
и ![]() связаны операции симметрии
связаны операции симметрии ![]() и
и ![]() . Множество операций симметрии молекулы аммиака может быть обозначено следующим образом:
. Множество операций симметрии молекулы аммиака может быть обозначено следующим образом:![]() .
.





![]() и
и ![]() будем понимать их последовательное выполнение. Первые два требования к алгебраической операции, очевидно, выполняются. Проверим выполнение третьего условия из определения алгебраической операции.
будем понимать их последовательное выполнение. Первые два требования к алгебраической операции, очевидно, выполняются. Проверим выполнение третьего условия из определения алгебраической операции.