Дипломная работа: Теория симметрии молекул
Теорема 3. Если G – абелева группа и G@G¢, то и G¢ - абелева группа.
Теорема 4. Каждая конечная группа изоморфна некоторой группе перестановок и некоторой группе матриц.
Приведем пример. Пронумеруем элементы группы C3 V в виде 
=1; 
=2; 
=3; 
=4; 
=5; 
=6. Используя таблицу Кэли группы C3 V , запишем
.
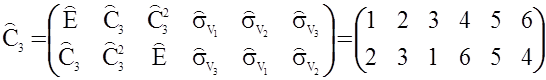Далее, получим, используя правило умножения перестановок. Ясно, что
.
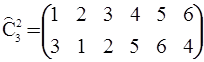Аналогично получаем остальные четыре перестановки искомой группы: , 
, , . Мы получили другое выражение группы C3 V : ее представление в виде группы перестановок.
1.3 Классы смежности и классы сопряженных элементов
Пусть G – группа, H – ее подгруппа.
Определение 1. Всякое множество Hg (т. е. совокупность всех элементов hg, где h пробегает H, g – фиксированный элемент группы G) называется правым смежным классом группы G по подгруппе H. Аналогично определение левого смежного класса gH.
Каждый элемент смежного класса называется его представлением. Так, элемент g – представитель класса Hg, поскольку из-за наличия в группе Н единицы е группы G элемент g=egÎHg.
Будем считать подгруппу H первым правым смежным классом. В результате группу G можно представить в виде объединения правых смежных классов:
Hg1 +Hg2 +…+Hgm =G(3)
Выражение (3) называется правосторонним разложением группы G по подгруппе H.
Рассмотрим пример. В группе C3 V выберем подгруппу {, 
}={}2 , считая ее первым правым смежным классом. Возьмем элемент и по таблице Кэли группы C3 V найдем второй правый смежный класс {, }={, 
}. Элемент не входит в оба класса, и с помощью его получаем третий правый смежный класс {, }={, 
}. Таким образом, правостороннее разложение группы C3 V по подгруппе {}2 имеет вид
C3 V ={, }+{, }+{, }. (4)
Аналогично левостороннее разложение группы C3 V по подгруппе {}2 имеет вид
C3 V ={, }+{, }+{,}. (5)
Существенно, что левостороннее разложение (5) не совпадает с правосторонним разложением (4).
Теорема Лагранжа. Порядок подгруппы H конечной группы G является делителем порядка группы G.
Теорема Лагранжа облегчает нахождение подгруппы группы G. Надо искать подгруппы группы G не любых порядков, а порядков, равных делителям порядка группы G. Например, группа C3 V имеет порядок 6, а у числа 6 делителями являются числа 1, 2, 3, 6. Мы уже нашли подгруппы группы C3 V , имеющие приведенные порядки – это подгруппы {}, {
}, {}3 ={, , } и сама C3 V . Подчеркнем, что если число m является делителем порядка группы G, то отсюда не следует, что в группе G есть подгруппа порядка m, т. е. теорема, обратная теореме Лагранжа, не имеет места.
Определение 2. Элементы а и b группы G называются сопряженными, если существует элемент х из группы G такой, что выполняется равенство
a=x-1 bx(6)
Например, в группе C3 V согласно таблице Кэли этой группы, имеем 
=-1 =
, поэтом элементы и 
сопряжены с помощью элемента .
С помощью понятия сопряженности можно дать классификацию элементов группы G. Обозначим через Kg1 , Kg2 , …, Kgt все классы сопряженных элементов. Всю группу G можно представить в виде
Kg1 + Kg2 + …+ Kgt =K1 +K2 +…+Kt =G, (7)
где Kgi =Ki ; i=1, 2, …, t – непересекающиеся классы сопряженных элементов.
Найдем эти классы для группы C3 V . Очевидно, что единица сама является классом сопряженных элементов, ибо всегда 
=. Обозначим этот класс R1 . Второй класс сопряженных элементов – это {, }, поскольку не сопряжено с и , а других возможностей нет. С помощью таблицы Кэли проверяется, что третий класс сопряженных элементов есть {
, 
, 
}, в итоге
C3 V = K1 +K2 +K3 ={}+{, }+{, , } (8)