Дипломная работа: Управление асинхронным двигателем

Общим недостатком законов с поддержанием постоянства потокосцепления являются: низкая надежность, обусловленная наличием датчиков, встраиваемых в двигатель, и потери в стали при работе двигателя с нагрузочным моментом меньше номинального. Эти потери вызваны необходимостью поддержания постоянного номинального потокосцепления в различных режимах работы.

Существенно повысить КПД двигателя можно путем регулирования магнитного потока статора (ротора) в зависимости от величины нагрузочного момента (скольжения). Недостатками такого управления являются низкие динамические характеристики привода, обусловленные большой величиной постоянной времени ротора, из-за чего магнитный поток машины восстанавливается с некоторой задержкой и сложность технической реализации системы управления.

На практике группа законов с постоянством магнитного потока получила распространение для динамичных электроприводов, работающих с постоянным моментом сопротивления на валу и с частыми ударными приложениями нагрузки. В то время как группа законов с регулированием магнитного потока в функции нагрузки на валу применяется для низкодинамичных электроприводов и для приводов с “вентиляторной” нагрузкой.

В то же время существует ряд приводов таких механизмов как насосы, компрессоры, конвейеры и т. д., которые занимают промежуточное положение между динамичными и низкодинамичными, и для которых существующие системы не в полной мере удовлетворяют предъявляемым к этим приводам требованиям. Высокодинамичные привода имеют сложную систему управления и повышенные энергетические потери при недогрузе двигателей, а низкодинамичные привода не всегда способны отработать быстрые изменения статического момента.

На основании вышесказанного можно сделать вывод, что существующие системы не в полной мере отвечают требованиям, предъявляемым к электроприводам c асинхронными двигателями.

Учитывая, что в настоящее время большинство приводов таких механизмов как вентиляторы, насосы, компрессоры и т. д. имеют нерегулируемый привод, актуальной является задача выбора системы управления. Причем система управления должна обеспечивать достаточно высокое быстродействие, надежность и высокие энергетические характеристики привода.

Как уже было отмечено, высокими энергетическими характеристиками обладают системы с регулированием магнитного потока в функции нагрузки. Увеличить их динамические характеристики можно путем форсировки статорного напряжения (тока) во время переходных процессов и частых формирований управляющих воздействий. Получить высокую надежность можно за счет применения упрощенной системы регулирования, отказа от встроенных в двигатель и механически связанных с ротором датчиков.

На рис. показана структурная схема системы, поддерживающей постоянство угла между векторами тока статора (I₁₎ и потокосцепления ротора (Y₂₎ , что равнозначно поддержанию постоянства относительного скольжения двигателя. Система управления состоит из: задатчика интенсивности (1); программируемого контроллера (2); блока широтно - импульсного модулятора (3); асинхронного электродвигателя с короткозамкнутым ротором (4); датчика тока (5) и блока определения угла (6). Поддержание постоянства угла между I₁ и Y₂ обеспечивает работу двигателя в области номинального режима с максимальными значениями КПД и cos(j). Кроме того, привод, обладая абсолютно жесткой механической характеристикой, что обусловлено постоянством относительного скольжения, получает возможность точного регулирования скорости вращения ротора путем изменения частоты поля.

Для технической реализации системы с поддержанием постоянства коэффициента полезного действия электродвигателя необходимо знать либо мгновенные величины относительного скольжения либо величину угла между током статора и потокосцеплением ротора. Измерить скольжение можно с помощью электромеханического или цифрового датчика скорости, угол между I₁ и Y₂ - с помощью датчиков напряжения и датчиков фазных токов. Так как датчик скорости существенно повышает стоимость системы регулирования, эксплуатационные затраты и ухудшает общую надежность системы, то более предпочтителен вариант системы с обратной связью по углу между векторами тока статора и потокосцепления ротора.

Существующие в настоящее время методы определения угла между I₁ и Y₂ , например [1, 2, 3], имеют низкое быстродействие (не более шести измерений искомого угла за один оборот вектора поля) и невысокую точность измерения, обусловленную “дрейфом нуля” аналоговых элементов схемы и вводом в алгоритм определения углов активного сопротивления статора, значение которого изменяется в широких пределах при нагреве двигателя.

Рассмотрим алгоритм определения угла между I₁ и Y₂ , лишенный вышеуказанных недостатков. Для обоснования алгоритма построим векторную диаграмму асинхронного двигателя с короткозамкнутым ротором, отложив вдоль действительной оси R_a ток намагничивания I₀ , определенный по известным реактивным параметрам асинхронного двигателя и измеренным значениям фазных токов и напряжений [4].

Значение углов между I₁ и Y₂ можно определить в реальном масштабе времени, когда вращение вектора тока статора статора I₁ определяется частотой питания асинхронного двигателя и в ускоренном масштабе времени, когда вращение вектора тока I₁ определяется в модели выбранным шагом временного интервала и быстродействием микропроцессорной системы. Второй вариант измерения углов более предпочтителен, так как позволяет осуществить больше измерений. По измеренным значениям фазных токов двигателя определяем величину вектора тока I₁ и совмещаем его в модели с действительной осью Ra, а затем переводим (в произвольный момент времени t₁ ) вектор тока I₁ в неподвижную, относительно статора, систему координат, то есть начинает выполняться программа, согласно которой вектор тока I₁ поворачивается против часовой стрелки со скоростью, определяемой быстродействием микропроцессорной системы и выбранным шагом временного интервала.

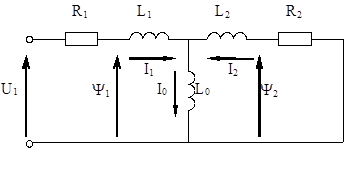
Из Т-образной схемы замещения (рис. 3) видно, что , то есть векторы тока и потокосцепления ротора взаимно перпендикулярны. В процессе поворота угол между векторами I₀ и Y₂ g(t) будет изменяться согласно выражения: (1), где a=w₀ t - текущий угол между вектором тока статора и действительной осью Ra. В момент времени t₂ вектор тока статора I₁ займет положение OC, при котором векторы тока ротора I₂ и потокосцепления ротора Y₂ взаимно перпендикулярны, то есть g(t₂ )=g.

Из рис. видно, что при g(t₂ )=g выполняется соотношение:

I₁ ×sinb=BC=AC+AB.

Величина отрезка AB определяется из подобия треугольников OBA и OED: .

Так как AC = i₂ (из векторной диаграммы), то

BC = I₂ + = .

Величина отрезка AC определяется из треугольника АFC:

(2).

Таким образом, изменяющийся во времени угол g(t) будет равен углу между векторами тока намагничивания I₀ и потокосцепления ротора Y₂ асинхронного двигателя в момент выполнения равенства:

. (3)

Из векторной диаграммы (рис. ) видно, что искомый угол b между векторами тока статора I₁ и потокосцепления ротора Y₂ будет определяться как:

b = a(t₂ ) + g(t2) = w₀ ×t + g

2. ТЕХНИЧЕСКОЕ ЗАДАНИЕ

2.1 Наименование и область применения

Разрабатываемое устройство называется: автоматическая система управления асинхронным двигателем.