Дипломная работа: Возвратные задачи
С помощью рекуррентных соотношений можно задать следующие последовательности:
1). Геометрическая прогрессия
un +1 = q∙un
2). Арифметическая прогрессия
un +1 = un + d
другой вид un +2 = 2∙un +1 − un
3). Последовательность чисел Фиббоначи
un +2 = un +1 +un
4). Последовательность квадратов натуральных чисел
un +1 = un + 2∙n + 1
другой вид un +3 = 3∙un +2 − 3∙un +1 + un
5). Последовательность кубов натуральных чисел
un +4 = 4∙un +3 − 6∙un +2 +4∙un +1 − un
6). Все периодические последовательности: u1 , u2 , …, uk +1 , …
un + k = un .
Также рекуррентные соотношения могут использоваться при решении задач (в частности, при доказательстве равенств):
7). Интегрирование простейших рациональных дробей IVтипа
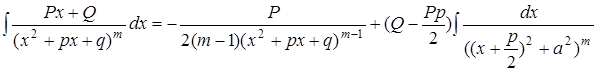
![]()
ОбозначимIm = 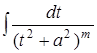 , где t = x+
, где t = x+![]()
Im = 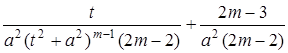 ∙Im-1
∙Im-1
8). ИнтегралIn =![]()
In =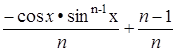 ∙In-2
∙In-2
9). Формула длины стороны при удвоении числа сторон правильного вписанного многоугольника
an =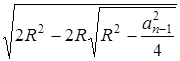 , при n≥ 2
, при n≥ 2
R– радиус описанной окружности
Если сторона a1 исходного правильного вписанного многоугольника задана, то an есть сторона многоугольника, полученного из исходного (n-1) кратным удвоением числа сторон.
10). Дифференциальные уравнения высших порядков
y( n ) = f(x, y, y', y», …, y( n -1) )
11). Определитель Вандермонда