Дипломная работа: Возвратные задачи

∆ (x₁ , x₂ , …, x_n ) =(x_n −x₁ )(x_{n -1} −x₁ )…(x₂ −x₁ )∙∆(x₂ , x₃ , …,x_n ).

Глава 1

1.1. Задача о ханойской башне

Рассмотрим сначала маленькую изящную головоломку под названием ханойская башня, которую придумал французский математик Эдуард Люка в 1883 г. Башня представляет собой восемь дисков, нанизанных в порядке уменьшения размеров на один из трех колышков. Задача состоит в том, чтобы переместить всю башню на один из других колышков, перенося каждый раз только один диск, и не помещая больший диск на меньший.

Будем решать эту задачу в общем виде, т.е. посмотрим, что будет в случае n дисков.

Будем говорить, что T_n есть минимальное число перекладываний, необходимых для перемещения n дисков с одного колышка на другой по правилам Люка.

Рассмотрим крайние случаи: Т₀ =0, T₁ =1, T₂ =3, T₃ =7. Эксперимент с тремя дисками дает ключ к общему правилу перемещения n дисков: сначала мы перемещаем (n−1) меньших дисков на любой из колышков (что требует Т_{n -1} перекладываний), затем перекладываем самый большой диск (одно перекладывание ) и, наконец, помещаем (n−1) меньших дисков обратно на самый большой диск (еще Т_{n -1} перекладываний). Таким образом, n дисков (при n>0) можно переместить самое большое за 2T_{n -1} +1 перекладываний (т.е. достаточно перекладываний): T_n ≤ 2T_{n -1} +1.

Сейчас покажем, что необходимо 2T_{n -1} +1 перекладываний. На некотором этапе мы обязаны переместить самый большой диск. Когда мы это делаем, (n−1) меньших дисков должны находиться на одном колышке, а для того чтобы собрать их вместе, потребуется по меньшей мере Т_{n -1} перекладываний. Самый большой диск можно перекладывать и более одного раза. Но после перемещения самого большого диска в последний раз мы обязаны поместить (n−1) меньших дисков (которые опять должны находиться на одном колышке) обратно на наибольший диск, что также требует Т_{n -1} перекладываний. Следовательно, T_n ≥ 2T_{n -1} +1.

Эти два неравенства вместе с тривиальным решением при n=0 дают рекуррентное соотношение:

(1)

?₀ =0

T_n = 2T_{n -1} +1 при n>0

При достаточно большом n для вычисления Т_n потребуется слишком много времени, поэтому получим Т_n в простой, компактной, «замкнутой форме», что позволит вычислить Т_n быстро.

Первый способ решения (угадывание правильного решения с последующим доказательством, что наша догадка верна).

Вычислим: Т₃ =2∙3+1=7; Т₄ =2∙7+1; Т₅ =2∙15+1; Т₆ =2∙31+1=63. Теперь можно сделать предположение, что

Т_n =2ⁿ − 1 при n≥0. (2)

Докажем методом математической индукции по числу n:

1) База: n=0, Т₀ =2⁰ –1=1–1=0 (верно);

2) Индуктивный переход: пусть доказано для всех чисел t≤ (n–1). Докажем для t=n: Т_n = 2T_{n -1} +1 2(2^{n -1} −1)+1 = 2∙2^{n -1} −2+1 = 2ⁿ − 1

Из пунктов 1 и 2 следует: при n≥0 Т_n = 2ⁿ − 1

Второй способ решения.

К обеим частям соотношения (1) прибавим 1:

Т₀ +1 = 1,

Т_n +1 = 2T_{n -1} +2 при n>0.

Обозначим U_n = T_n +1, тогда получим

U₀ = 1

U_n = 2U_{n -1} при n>0.

Решением этой рекурсии есть U_n =2ⁿ ; следовательно Т_n = 2ⁿ −1.

1 .2. Задача о разрезании пиццы

Формулировка задачи: сколько кусков пиццы можно получить, делая n прямолинейных разрезов ножом? Или, каково максимальное число L_n областей, на которые плоскость делится n прямыми?

1

????? ?????? ? ???????????? ??????? ???????.

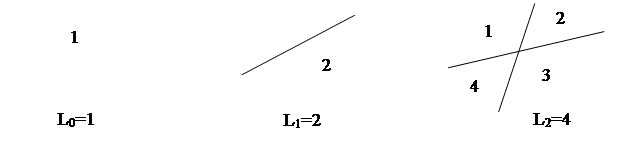
Эксперимент с тремя прямыми показывает, что добавленная третья прямая может рассекать самое большое три старых области вне зависимости от того, как расположены первые две прямые:

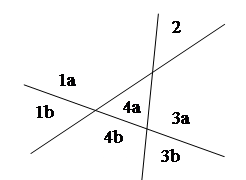Таким образом, L₃ =4+3=7 – самое большое, что можно сделать.

Обобщая, приходим к следующему выводу: новая n-я прямая (при n>0) увеличивает число областей на k- когда рассекает k старых областей - когда пересекает прежние прямые в (k−1) различных местах. Две прямые могут пересекаться не более чем в одной точке. Поэтому новая прямая может пересекать (n−1) старых прямых не более чем в (n−1) различных точках, и мы должны иметь k ≤ n. Установлена верхняя граница:

L_n ≤ L_{n -1} + n при n>0